练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．已知几个命题：①若点P不在平面α内，A、B、C三点都在平面α内，则P、A、B、C四点不在同一平面内；②两两相交的三条直线在同一平面内；③两组对边分别相等的四边形是平行四边形．其中正确命题的个数是（　　）
    A．0B．1C．2D．3

    分析 根据平面的基本性质进行判断①的正误共点的三条直线可能不共面，由此能判断②的正误；将平行四边形沿其对角线翻折一个适当的角度后折成一个空间四边形，两组对边仍然相等，但四个点不共面，由此能判断③的正误．

    解答 解：在①中：根据平面的基本性质得直线与直线外一点确定一个平面，
    若在平面α内，A、B、C三点共线，则P、A、B、C四点在同一平面内．故①不正确；
    在②中：共点的三条直线可能不共面，如教室墙角处两两垂直相交的三条直线就不共面，故②不正确；
    在③中：将平行四边形沿其对角线翻折一个适当的角度后折成一个空间四边形，两组对边仍然相等，但四个点不共面，
    连平面图形都不是，所以不是平行四边形，故③不正确．
    故选：A．

    点评 本题考查命题真假的判断，是基础题，解题时要认真审题，注意平面的基本性质及推论的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．已知f （x）=x3+3ax2+3（a+2）x+1有极大值和极小值，则a的取值范围是（　　）
    A．（-∞，-1）∪（2，+∞）B．（-2，1）C．（1，2）D．（-∞，-2）∪（1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=a-$\frac{1}{{{2^x}+1}}$的图象经过点（0，$\frac{1}{2}$）．
    （1）求函数y=f（x）的解析式；
    （2）求证：f（x）+f（-x）=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数，得到如下资料：
    日期12月1日12月2日12月3日12月4日12月5日
    温差x （℃）101113128
    发芽数y（颗）2325302616
    该农科所确定的研究方案是：先从这五组数据中选取2组，用剩下的3组数据求线性回归方程，再对被选取的2组数据进行检验．
    （1）求选取的2组数据恰好是不相邻2天数据的概率；
    （2）若选取的是12月1日与12月5日的两组数据，请根据12月2日至12月4日的数据，求出y关于x的线性回归方程$\stackrel{∧}{y}$=bx+a已知回归直线方程是：$\stackrel{∧}{y}$=bx+a，其中b=$\frac{\sum_{i-1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i-1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$；
    （3）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（2）中所得的线性回归方程是否可靠？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．下列三个结论中正确的有①②（填序号）．
    ①函数f（x）=lg（x+1）+lg（x-1）的定义域是（1，+∞）；
    ②若幂函数f（x）的图象经过点（2，4），则该函数为偶函数；
    ③函数y=5|x|的值域是（0，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．将参数方程$\left\{\begin{array}{l}x=-2+{cos^2}θ\\ y={cos^2}θ\end{array}\right.$（θ为参数）化为普通方程为（　　）
    A．y=x-2B．y=x-2（0≤y≤1）C．y=x+2（-2≤x≤-1）D．y=x+2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．某农科所种植的甲、乙两种水稻，连续六年在面积相等的两块稻田中作对比试验，试验得出平均产量是$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$=415㎏，方差是s甲2=794，s乙2=958，那么这两个水稻品种中产量比较稳定的是甲．（填甲或乙）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

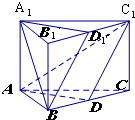    1．如图所示，已知三棱柱ABC-A1B1C1中，D是BC的中点，D1是B1C1的中点，设平面A1D1B∩平面ABC=l1，平面ADC1∩平面A1B1C1=l2，求证：l1∥l2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．若点P从（1，0）出发，沿单位圆x2+y2=1按逆时针方向匀速运动，且角速度是ω=$\frac{π}{6}$弧度/秒，t秒钟时运动到Q点．
    （1）当t=4，求点Q的坐标；
    （2）当0≤t≤6，求弦PQ的长（用t表示）．

    查看答案和解析>>

    同步练习册答案