Question

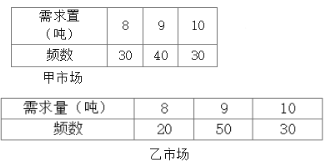
【题目】某蔬菜批发商分别在甲、乙两市场销售某种蔬菜（两个市场的销售互不影响），己知该蔬菜每售出1吨获利500元，未售出的蔬菜低价处理，每吨亏损100 元.现统计甲、乙两市场以往100个销售周期该蔬菜的市场需求量的频数分布，如下表:

以市场需求量的频率代替需求量的概率.设批发商在下个销售周期购进吨该蔬菜，在 甲、乙两市场同时销售，以（单位：吨）表示下个销售周期两市场的需求量，(单位：元）表示下个销售周期两市场的销售总利润.

(Ⅰ)当时，求与的函数解析式，并估计销售利润不少于8900元的槪率；

(Ⅱ)以销售利润的期望为决策依据，判断与应选用哪—个.

Answer 1

【答案】(Ⅰ)解析式见解析；槪率为0.71；(Ⅱ) .

【解析】

(Ⅰ) 根据题意可得解析式为分段函数．分析题意可得当时可满足利润不少于8900元，求出的概率后再根据对立事件的概率公式求解即可． (Ⅱ) 结合题意中的销售情况，分别求出当和时的销售利润的期望，比较后可得结论．

(Ⅰ)由题意可知，当，；

当，，

所以与的函数解析式为.

由题意可知，一个销售周期内甲市场需求量为8,9,10的概率分别为0.3,0.4,0.3；乙市场需求量为8，9，10的概率分别为0.2，0.5，0.3.

设销售的利润不少于8900元的事件记为.

当，，

当，，解得，

所以．

由题意可知，；

；

所以.

(Ⅱ)由题意得，，

，，

．

①当时，

；

②当时，

．

因为，

所以应选．