
【题目】如图所示,在四棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
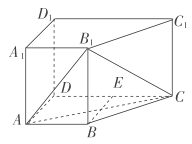
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,证明出四边形
,证明出四边形![]() 为平行四边形,由此可得出
为平行四边形,由此可得出![]() 各边边长,利用勾股定理逆定理可证明出
各边边长,利用勾股定理逆定理可证明出![]() ,进而得出
,进而得出![]() ,再由侧棱
,再由侧棱![]() 底面
底面![]() ,可得出
,可得出![]() ,利用线面垂直的判定定理可证明出
,利用线面垂直的判定定理可证明出![]() 平面
平面![]() ;
;
(2)以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 的方向为
的方向为![]() 、
、![]() 、
、![]() 轴的正方向建立空间直角坐标系,计算出平面
轴的正方向建立空间直角坐标系,计算出平面![]() 的一个法向量,利用空间向量法可求出直线
的一个法向量,利用空间向量法可求出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
![]() ,
,![]() ,
,![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() 且
且![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,即
,即![]() ,又
,又![]() ,所以
,所以![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
又![]() ,
,![]() 平面
平面![]() ;
;
(2)以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 的方向为
的方向为![]() 、
、![]() 、
、![]() 轴的正方向建立如图所示的空间直角坐标系,则
轴的正方向建立如图所示的空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
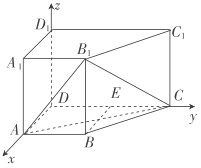
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,则由
,则由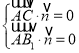 ,得
,得![]() ,
,
取![]() ,得
,得![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则 .
.
因此,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】一个简单图中两两相邻的t个项点称为一个团,与其余每个顶点均相邻的顶点称为中心点.给定整数![]() 及满足
及满足![]() 的整数k,一个n阶简单图G中不存在k+1团,其全部k团记为
的整数k,一个n阶简单图G中不存在k+1团,其全部k团记为![]() .
.
(1)证明:![]() ;
;
(2)若在图G中再添加一条边就存在k+1团,求图G的中心点个数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为坐标原点,动点
为坐标原点,动点![]() 在椭圆
在椭圆![]() :
:![]() 上,该椭圆的左顶点
上,该椭圆的左顶点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若椭圆![]() 外一点
外一点![]() 满足,
满足,![]() 平行于
平行于![]() 轴,
轴,![]() ,动点
,动点![]() 在直线
在直线![]() 上,满足
上,满足![]() .设过点
.设过点![]() 且垂直
且垂直![]() 的直线
的直线![]() ,试问直线
,试问直线![]() 是否过定点?若过定点,请写出该定点,若不过定点请说明理由.
是否过定点?若过定点,请写出该定点,若不过定点请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国式过马路”的大意是凑够一撮人即可走,跟红绿灯无关.部分法律专家的观点为“交通规则的制定目的就在于服务城市管理,方便行人,而‘中国式过马路’是对我国法治化进程的严重阻碍,反应了国人规则意识的淡薄.”某新闻媒体对此观点进行了网上调查,所有参与调查的人中,持“支持”“中立”和“不支持”态度的人数如表所示:
支持 | 中立 | 不支持 | |
20岁以下 | 700 | 450 | 200 |
20岁及以上 | 200 | 150 | 300 |
在所有参与调查的人中,用分层随机抽样的方法抽取![]() 人,则持“支持”态度的人中20岁及以上的有_________人
人,则持“支持”态度的人中20岁及以上的有_________人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语,在一轮活动中,如果两人都猜对,则“星队”得3分;如果只有一个人猜对,则“星队”得1分;如果两人都没猜对,则“星队”得0分。已知甲每轮猜对的概率是![]() ,乙每轮猜对的概率是
,乙每轮猜对的概率是![]() ;每轮活动中甲、乙猜对与否互不影响。各轮结果亦互不影响。假设“星队”参加两轮活动,求:
;每轮活动中甲、乙猜对与否互不影响。各轮结果亦互不影响。假设“星队”参加两轮活动,求:
(Ⅰ)“星队”至少猜对3个成语的概率;
(Ⅱ)“星队”两轮得分之和为X的分布列和数学期望EX.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com