
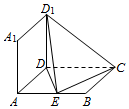
 如图,矩形ABCD所在的平面和正方形ADD1A1所在的平面互相垂直,AD=AA1=1,AB=2,点E在棱AB上移动.
如图,矩形ABCD所在的平面和正方形ADD1A1所在的平面互相垂直,AD=AA1=1,AB=2,点E在棱AB上移动.分析 (1)分别以DA,DC,DD1为x轴,y轴,z轴建立空间坐标系,利用向量法能求出点E到平面ACD1的距离.
(2)求出平面CED1的法向量和平面ECD的一个法向量,利用向量法能求出当AE=2-$\sqrt{3}$时,二面角D1-EC-D的大小为$\frac{π}{4}$.
解答 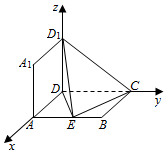 解:(1)分别以DA,DC,DD1为x轴,y轴,z轴建立空间坐标系,
解:(1)分别以DA,DC,DD1为x轴,y轴,z轴建立空间坐标系,
则E(1,1,0),A(1,0,0),C(0,2,0),D1(0,0,1).
$\overrightarrow{A{D_1}}=(-1,0,1)$,$\overrightarrow{AC}=(-1,2,0)$,
设点E到平面ACD1的距离为d,$\overrightarrow n=(x,y,z)$是平面ACD1的法向量,
由$\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{A{D_1}}=0}\\{\overrightarrow n•\overrightarrow{AC}=0}\end{array}}\right.$,得$\left\{{\begin{array}{l}{-x+z=0}\\{-x+2y=0}\end{array}}\right.$,取$\overrightarrow n=(2,1,2)$.
而$\overrightarrow{AE}=(0,1,0)$,
所以$d=\frac{{|\overrightarrow n•\overrightarrow{AE}|}}{|\overrightarrow n|}=\frac{1}{3}$.
(2)设AE=l(0<l<2),由(1)知E(1,l,0),
设$\overrightarrow{n_1}=({x_1},{y_1},{z_1})$是平面CED1的法向量.
$\overrightarrow{EC}=(-1,2-l,0)$,$\overrightarrow{C{D_1}}=(0,-2,1)$.
由$\left\{{\begin{array}{l}{\overrightarrow{n_1}•\overrightarrow{E{C_1}}=0}\\{\overrightarrow{n_1}•\overrightarrow{C{D_1}}=0}\end{array}}\right.$,得$\left\{{\begin{array}{l}{-{x_1}+(2-l){y_1}=0}\\{-2{y_1}+{z_1}=0}\end{array}}\right.$,取$\overrightarrow{n_1}=(2-l,1,2)$,
又平面ECD的一个法向量为$\overrightarrow m=(0,0,1)$.
由$cos\frac{π}{4}=\frac{{|\overrightarrow m•\overrightarrow{n_1}|}}{{|\overrightarrow m||\overrightarrow{n_1}|}}$,即$\frac{{\sqrt{2}}}{2}=\frac{2}{{\sqrt{{{(2-l)}^2}+5}}}$,
解得$l=2-\sqrt{3}$,即$AE=2-\sqrt{3}$.
点评 本题考查点到平面的距离的求法,考查满足条件的点的位置的判断,是中档题,解题时要认真审,注意向量法的合理运用.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | 36种 | B. | 54种 | C. | 72种 | D. | 118种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2≠kx+b(k,b为常数) | B. | ?x0∈R,x02<kx0+b(k,b为常数) | ||
| C. | ?x∈R,x2≥kx+b(k,b为常数) | D. | ?x0∈R,x02>kx0+b(k,b为常数) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com