
| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |
分析 求出$\frac{{{a_{n+1}}}}{a_n}=2$,从而数列{an}是等比数列,由a2=1,得到${a_n}=1×{2^{n-2}}$,由此能求出结果.
解答 解:因为${a_{n+1}}=2{a_n}(n∈{N^*})$,所以$\frac{{{a_{n+1}}}}{a_n}=2$,
所以数列{an}是等比数列,
因为a2=1,所以${a_n}=1×{2^{n-2}}$,
所以${a_{2015}}=1×{2^{2015-2}}={2^{2013}}$,
所以${log_2}{a_{2015}}={log_2}{2^{2013}}=2013$.
故选:B.
点评 本题考查等比数列的第2015项的对数的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
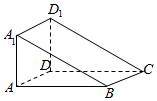 如图所示的几何体中,四边形ABCD是边长为$\sqrt{2}$的正方形,矩形ADD1A1所在的平面垂直于平面ABCD,且AA1=2,则该几何体ABCD-A1D1的外接球的体积是( )
如图所示的几何体中,四边形ABCD是边长为$\sqrt{2}$的正方形,矩形ADD1A1所在的平面垂直于平面ABCD,且AA1=2,则该几何体ABCD-A1D1的外接球的体积是( )| A. | $\frac{{2\sqrt{2}π}}{3}$ | B. | $\frac{{4\sqrt{2}π}}{3}$ | C. | $2\sqrt{2}π$ | D. | $\frac{{8\sqrt{2}π}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
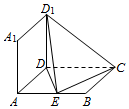 如图,矩形ABCD所在的平面和正方形ADD1A1所在的平面互相垂直,AD=AA1=1,AB=2,点E在棱AB上移动.
如图,矩形ABCD所在的平面和正方形ADD1A1所在的平面互相垂直,AD=AA1=1,AB=2,点E在棱AB上移动.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈R,使得x2+4x+6≥0,为真命题 | B. | ¬p:?x∈R,使得x2+4x+6≥0,为假命题 | ||
| C. | ¬p:?x∈R,使得x2+4x+6≥0,为真命题 | D. | ¬p:?x∈R,使得x2+4x+6≥0,为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com