
���� ��1������C����sin2��=2acos�ȣ�a��0��������2sin2��=2a��cos�ȣ�a��0������x=��cos�ȣ�y=��sin�ȴ��뼴�ɵó�ֱ�����귽�̣�ֱ��l�IJ�������Ϊ$\left\{{\begin{array}{l}{x=2+\frac{{\sqrt{2}}}{2}t}\\{y=\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$��tΪ����������ȥ����t��Ϊ��ͨ���̣�y=x-2��
��2����P��-2��-4����ֱ��l�ϣ��ɵ�ֱ��l�ı����̣�$\left\{\begin{array}{l}{x=-2+\frac{\sqrt{2}}{2}m}\\{y=-4+\frac{\sqrt{2}}{2}m}\end{array}\right.$�����������߷��̿ɵã�m2-$��8\sqrt{2}+\sqrt{2}a��$m+4a+32=0��|PM|=m1��|PN|=m2��|MN|=|m1-m2|=$\sqrt{��{m}_{1}+{m}_{2}��^{2}-4{m}_{1}{m}_{2}}$������|PM|��|MN|��|PN|�ɵȱ����У��ɵ�|MN|2=|PM|•|PN|�����ɵó���
��� �⣺��1������C����sin2��=2acos�ȣ�a��0��������2sin2��=2a��cos�ȣ�a��0�����ɵ�ֱ�����귽�̣�y2=2ax��a��0����
ֱ��l�IJ�������Ϊ$\left\{{\begin{array}{l}{x=2+\frac{{\sqrt{2}}}{2}t}\\{y=\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$��tΪ����������Ϊ��ͨ���̣�y=x-2��
��2����P��-2��-4����ֱ��l�ϣ��ɵ�ֱ��l�ı����̣�$\left\{\begin{array}{l}{x=-2+\frac{\sqrt{2}}{2}m}\\{y=-4+\frac{\sqrt{2}}{2}m}\end{array}\right.$�����������߷��̿ɵã�m2-$��8\sqrt{2}+\sqrt{2}a��$m+4a+32=0��
��=$��8\sqrt{2}+\sqrt{2}a��^{2}$-4��4a+32��=2a2+16a��0����a��0����
��m1+m2=$8\sqrt{2}+\sqrt{2}a$��m1m2=4a+32��
|PM|=m1��|PN|=m2��|MN|=|m1-m2|=$\sqrt{��{m}_{1}+{m}_{2}��^{2}-4{m}_{1}{m}_{2}}$=$\sqrt{��8\sqrt{2}+\sqrt{2}a��^{2}-4��4a+32��}$=$\sqrt{2{a}^{2}+16a}$��
��|PM|��|MN|��|PN|�ɵȱ����У�
��|MN|2=|PM|•|PN|��
��2a2+16a=m1m2=4a+32������a2+6a-16=0��a��0��
���a=2��
���� ���⿼���˼����귽�̻�Ϊֱ�����귽�̡��������̻�Ϊ��ͨ���̼���Ӧ�á��ҳ���ʽ���ȱ����е����ʣ�������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2012 | B�� | 2013 | C�� | 2014 | D�� | 2015 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
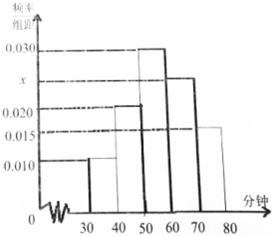 4��23���ǡ���������ա���ij��ѧ�ڴ��ڼ俪չ��һϵ�еĶ������������ü��������������ȡ��100��ѧ����������Ķ�ʱ����е��飬�����Ǹ��ݵ��������Ƶ�ѧ���վ������Ķ�ʱ�䣨��λ�����ӣ���Ƶ�ʷֲ�ֱ��ͼ�������վ������Ķ�ʱ�䲻����60���ӵ�ѧ����Ϊ�������ա�������60���ӵ�ѧ����Ϊ���Ƕ����ա�
4��23���ǡ���������ա���ij��ѧ�ڴ��ڼ俪չ��һϵ�еĶ������������ü��������������ȡ��100��ѧ����������Ķ�ʱ����е��飬�����Ǹ��ݵ��������Ƶ�ѧ���վ������Ķ�ʱ�䣨��λ�����ӣ���Ƶ�ʷֲ�ֱ��ͼ�������վ������Ķ�ʱ�䲻����60���ӵ�ѧ����Ϊ�������ա�������60���ӵ�ѧ����Ϊ���Ƕ����ա�| �Ƕ����� | ������ | �ϼ� | |
| �� | 15 | ||
| Ů | 45 | ||
| �ϼ� |
| P��K2��k0�� | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com