
分析 (1)把极坐标方程根据极坐标与直角坐标的互化公式,化为直角坐标方程.
(2)解方程组求得P、Q的坐标,利用点到直线的距离公式求得点O到直线PQ的距离d,可得△OPQ的面积为S=$\frac{1}{2}$•PQ•d的值.
解答 解:(1)曲线C:ρ2+ρ2sin2θ-2=0化为直角坐标方程为x2+2y2-2=0,即$\frac{{x}^{2}}{2}$+y2=1,表示一个椭圆.
(2)由$\left\{\begin{array}{l}{x-y=1}\\{\frac{{x}^{2}}{2}{+y}^{2}=1}\end{array}\right.$ 求得$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$,或$\left\{\begin{array}{l}{x=\frac{4}{3}}\\{y=\frac{1}{3}}\end{array}\right.$,故可设P(0,-1)、Q($\frac{4}{3}$,$\frac{1}{3}$),
故点O到直线PQ:x-y-1=0的距离为d=$\frac{|0-0-1|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
△OPQ的面积为S=$\frac{1}{2}$•PQ•d=$\frac{1}{2}$•$\frac{4\sqrt{2}}{3}$•$\frac{\sqrt{2}}{2}$=$\frac{2}{3}$.
点评 本题主要考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,属于基础题.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:解答题
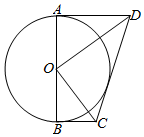 如图,AB是⊙O的直径,DA⊥AB,CB⊥AB,DO⊥CO
如图,AB是⊙O的直径,DA⊥AB,CB⊥AB,DO⊥CO查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com