
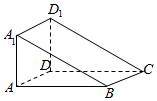
 如图所示的几何体中,四边形ABCD是边长为$\sqrt{2}$的正方形,矩形ADD1A1所在的平面垂直于平面ABCD,且AA1=2,则该几何体ABCD-A1D1的外接球的体积是( )
如图所示的几何体中,四边形ABCD是边长为$\sqrt{2}$的正方形,矩形ADD1A1所在的平面垂直于平面ABCD,且AA1=2,则该几何体ABCD-A1D1的外接球的体积是( )| A. | $\frac{{2\sqrt{2}π}}{3}$ | B. | $\frac{{4\sqrt{2}π}}{3}$ | C. | $2\sqrt{2}π$ | D. | $\frac{{8\sqrt{2}π}}{3}$ |
分析 将该几何体补成一个长方体ABCD-A1B1C1D1,该几何体ABCD-A1D1的外接球就是长方体ABCD-A1B1C1D1外接球,可得球的直径,即可求出该几何体ABCD-A1D1的外接球的体积.
解答 解:将该几何体补成一个长方体ABCD-A1B1C1D1,
该几何体ABCD-A1D1的外接球就是长方体ABCD-A1B1C1D1外接球,
所以球的直径是$\sqrt{{{(\sqrt{2})}^2}+{{(\sqrt{2})}^2}+{2^2}}=2\sqrt{2}$,
所以该几何体ABCD-A1D1的外接球的体积$\frac{4}{3}π{(\sqrt{2})^3}=\frac{{8\sqrt{2}π}}{3}$.
故选:D.
点评 本题考查该几何体ABCD-A1D1的外接球的体积,考查学生的计算能力,将该几何体补成一个长方体ABCD-A1B1C1D1是关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{15}{4}$ | B. | $\frac{15}{2}$ | C. | -$\frac{15}{4}$ | D. | -$\frac{15}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 32或-32 | C. | 64 | D. | 64或-64 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高血压 | 非高血压 | 总计 | |
| 年龄20到39 | 12 | c | 100 |
| 年龄40到60 | b | 52 | 100 |
| 总计 | 60 | a | 200 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2≠kx+b(k,b为常数) | B. | ?x0∈R,x02<kx0+b(k,b为常数) | ||
| C. | ?x∈R,x2≥kx+b(k,b为常数) | D. | ?x0∈R,x02>kx0+b(k,b为常数) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com