
| ��Ѫѹ | �Ǹ�Ѫѹ | �ܼ� | |
| ����20��39 | 12 | c | 100 |
| ����40��60 | b | 52 | 100 |
| �ܼ� | 60 | a | 200 |
| P��K2��k�� | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
���� ��1����12+c=100��b+12=60����� a��b��cֵ���Ӷ��õ�2��2���������������K2��10.828���ɴ���99.9%�İ�����Ϊ��Ѫѹ�������йأ�
��2���ɷֲ��������֪������20��39�Ļ����г�ȡ������Ϊ2��������40��60�Ļ����г�ȡ������Ϊ8�������⣬X��ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�������
��� �⣺��1����12+c=100��b+12=60��
���c=88��b=48��a=52+c=140��
�Ӷ��õ�2��2��������
| ��Ѫѹ | �Ǹ�Ѫѹ | �ܼ� | |
| ����20��39 | 12 | 88 | 100 |
| ����40��60 | 48 | 52 | 100 |
| �ܼ� | 60 | 140 | 200 |
| X | 0 | 1 | 2 |
| P | $\frac{28}{45}$ | $\frac{16}{45}$ | $\frac{1}{45}$ |
���� ���⿼������Լ����Ӧ�ã�������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�


 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | 3 | C�� | 2 | D�� | 4$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=-x2 | B�� | y=${log}_{\frac{1}{2}}$x | C�� | y=��$\frac{1}{2}$��x | D�� | y=x-$\frac{1}{x}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
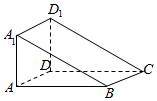 ��ͼ��ʾ�ļ������У��ı���ABCD�DZ߳�Ϊ$\sqrt{2}$�������Σ�����ADD1A1���ڵ�ƽ�洹ֱ��ƽ��ABCD����AA1=2����ü�����ABCD-A1D1������������ǣ�������
��ͼ��ʾ�ļ������У��ı���ABCD�DZ߳�Ϊ$\sqrt{2}$�������Σ�����ADD1A1���ڵ�ƽ�洹ֱ��ƽ��ABCD����AA1=2����ü�����ABCD-A1D1������������ǣ�������| A�� | $\frac{{2\sqrt{2}��}}{3}$ | B�� | $\frac{{4\sqrt{2}��}}{3}$ | C�� | $2\sqrt{2}��$ | D�� | $\frac{{8\sqrt{2}��}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
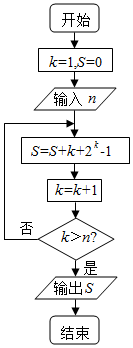
| A�� | 17 | B�� | 36 | C�� | 52 | D�� | 72 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com