
分析 由分段函数得到f[($\frac{1}{2}}$)${\;}^{\frac{1}{2}}$]=f($\frac{\sqrt{2}}{2}$)=f(2×$\frac{\sqrt{2}}{2}$)=f($\sqrt{2}$),由此能求出结果.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{log_2}x,x≥1\\ f({2x}),0<x<1\end{array}$,
∴f[($\frac{1}{2}}$)${\;}^{\frac{1}{2}}$]=f($\frac{\sqrt{2}}{2}$)=f(2×$\frac{\sqrt{2}}{2}$)=f($\sqrt{2}$)=$lo{g}_{2}\sqrt{2}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:解答题
| 高血压 | 非高血压 | 总计 | |
| 年龄20到39 | 12 | c | 100 |
| 年龄40到60 | b | 52 | 100 |
| 总计 | 60 | a | 200 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2≠kx+b(k,b为常数) | B. | ?x0∈R,x02<kx0+b(k,b为常数) | ||
| C. | ?x∈R,x2≥kx+b(k,b为常数) | D. | ?x0∈R,x02>kx0+b(k,b为常数) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
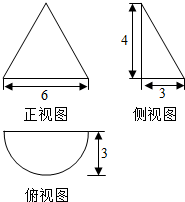
| A. | 12πcm2 | B. | 24πcm2 | C. | (15π+12)cm2 | D. | (12π+12)cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
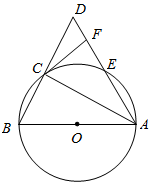 已知AB是圆O的直径,点C在圆O上(异于点A,B),连接BC并延长至点D,使得BC=CD,连接DA交圆O于点E,过点C作圆O的切线交AD于点F.
已知AB是圆O的直径,点C在圆O上(异于点A,B),连接BC并延长至点D,使得BC=CD,连接DA交圆O于点E,过点C作圆O的切线交AD于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com