
| A. | $\sqrt{2}$ | B. | 3 | C. | 2 | D. | 4$\sqrt{3}$ |
分析 设CA=b,则BC=$\sqrt{3}$b,利用余弦定理可求得cos2A=$\frac{4}{{b}^{2}}$+$\frac{{b}^{2}}{16}$-1,再利用三角形的面积公式可求得S△ABC=2bsinA,继而可求S△ABC2=48-$\frac{1}{4}$(b2-16)2,从而可得△ABC面积的最大值.
解答 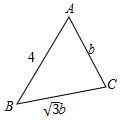 解:依题意,设CA=b,则BC=$\sqrt{3}$b,又AB=4,
解:依题意,设CA=b,则BC=$\sqrt{3}$b,又AB=4,
由余弦定理得:cosA=$\frac{{4}^{2}+{b}^{2}-(\sqrt{3}b)^{2}}{2×4×b}$=$\frac{8-{b}^{2}}{4b}$=$\frac{2}{b}$-$\frac{b}{4}$,
∴cos2A=($\frac{2}{b}$-$\frac{b}{4}$) 2=$\frac{4}{{b}^{2}}$+$\frac{{b}^{2}}{16}$-1,
∴sin2A=1-cos2A=2-$\frac{4}{{b}^{2}}$-$\frac{{b}^{2}}{16}$.
∵S△ABC=$\frac{1}{2}$AB•ACsinA=$\frac{1}{2}$×4bsinA=2bsinA,
∴S2△ABC=4b2sin2A=4b2(2-$\frac{4}{{b}^{2}}$-$\frac{{b}^{2}}{16}$)=48-$\frac{1}{4}$(b2-16)2,
当b2=16,即b=4时,4、4、4$\sqrt{3}$能组成三角形,
∴S2max=48,
∴Smax=4$\sqrt{3}$.
故选:D.
点评 本题考查余弦定理与正弦定理的应用,着重考查转化思想与二次函数的配方法,求得S2△ABC=48-$\frac{1}{4}$(b2-16)2是关键,也是难点,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 32或-32 | C. | 64 | D. | 64或-64 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高血压 | 非高血压 | 总计 | |
| 年龄20到39 | 12 | c | 100 |
| 年龄40到60 | b | 52 | 100 |
| 总计 | 60 | a | 200 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com