
分析 (1)求导,根据函数单调性求得函数f(x)的最大值,由f(x)max≥m,即可求得m的取值范围;
(2)求得g(x)的导函数g′(x),求得函数的单调性与最值,从而求得p的最小值.
解答 解:(1)∵$f'(x)=2({1+x})-\frac{2}{x+1}$,且当x≥0时,$1+x≥\frac{1}{x+1}$,
∵$f'(x)=2({1+x})-\frac{2}{x+1}$在[0,e-1]上有f'(x)≥0,
f(x)=(1+x)2-2ln(1+x)在[0,e-1]上单调递增,
得$f{(x)_{max}}=f({e-1})={e^2}-2$,
因为关于x的不等式f(x)-m≥0在[0,e-1](e为自然对数的底数) 上有实数解,
∴f(x)max≥m,即m≤e2-2,
所以实数m的取值范围是(-∞,e2-2].
(2)∵g(x)=f(x)-x2-1=2x-2ln(1+x),
∴$g'(x)=2({1-\frac{1}{x+1}})$,
∵$g'(x)=2({1-\frac{1}{x+1}})$,在(-1,0)上g'(x)<0,在(0,+∞),g'(x)>0,
∴g(x)min=g(0)=0,
∵x的方程g(x)=p至少有一个解,
∴p≥0,p最小值为0.
点评 本题考查利用导数研究函数的单调性及最值,考查函数恒成立问题,考查分析问题及解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高血压 | 非高血压 | 总计 | |
| 年龄20到39 | 12 | c | 100 |
| 年龄40到60 | b | 52 | 100 |
| 总计 | 60 | a | 200 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
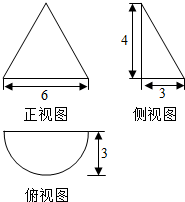
| A. | 12πcm2 | B. | 24πcm2 | C. | (15π+12)cm2 | D. | (12π+12)cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com