
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 恰有一个极值点,求实数a的取值范围;
恰有一个极值点,求实数a的取值范围;
(2)当![]() ,且
,且![]() 时,证明:
时,证明:![]() .(常数
.(常数![]() 是自然对数的底数).
是自然对数的底数).
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】双十一购物狂欢节,源于淘宝商城(天猫)![]() 年
年![]() 月
月![]() 日举办的网络促销活动,目前已成为中国电子商务行业的年度盛事,某商家为了解“双十一”这一天网购者在其网店一次性购物情况,从这一天交易成功的所有订单里随机抽取了
日举办的网络促销活动,目前已成为中国电子商务行业的年度盛事,某商家为了解“双十一”这一天网购者在其网店一次性购物情况,从这一天交易成功的所有订单里随机抽取了![]() 份,按购物金额(单位:元)进行统计,得到如下频率分布直方图(同一组中的数据用该组区间的中点值做代表计算).
份,按购物金额(单位:元)进行统计,得到如下频率分布直方图(同一组中的数据用该组区间的中点值做代表计算).
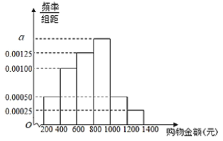
(1)求![]() 的值;
的值;
(2)试估计购物金额的平均数;
(3)若该商家制订了两种不同的促销方案:
方案一:全场商品打八折;
方案二:全场商品优惠如下表:
购物金额范围 |
|
|
|
|
|
|
商家优惠(元) |
|
|
|
|
|
|
如果你是购物者,你认为哪种方案优惠力度更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.
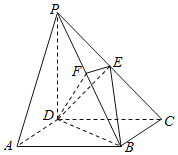
(1)求证:PA∥平面BDE;
(2)求证:PB⊥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为R,且对于任意x∈R,都有
的定义域为R,且对于任意x∈R,都有![]() 及
及![]() 成立,当
成立,当![]() 且
且![]() 时,都有
时,都有![]() 成立,下列四个结论中不正确命题是( )
成立,下列四个结论中不正确命题是( )
A.![]() B.函数
B.函数![]() 在区间
在区间![]() 上为增函数
上为增函数
C.直线![]() 是函数
是函数![]() 的一条对称轴D.方程
的一条对称轴D.方程![]() 在区间
在区间![]() 上有4个不同的实根
上有4个不同的实根
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 上位于第一象限内的任意一点,
上位于第一象限内的任意一点,![]() 为坐标原点,
为坐标原点,![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,![]() ,圆
,圆![]() :
:![]() .
.
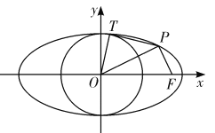
(1)求椭圆![]() 和圆
和圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作
作![]() 与圆
与圆![]() 相切于点
相切于点![]() ,使得点
,使得点![]() ,点
,点![]() 在
在![]() 的两侧.求四边形
的两侧.求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,从参加环保知识竞赛的学生中抽出![]() 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
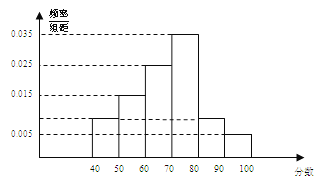
(1)![]() 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛成绩的平均数、众数、中位数。(不要求写过程)
(3) 从成绩是80分以上(包括80分)的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=![]() PD,则平面PQC与平面DCQ的位置关系为( )
PD,则平面PQC与平面DCQ的位置关系为( )

A. 平行 B. 垂直
C. 相交但不垂直 D. 位置关系不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图象关于直线
,其图象关于直线![]() 对称,为了得到函数
对称,为了得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象上的所有点( )
的图象上的所有点( )
A.先向左平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
B.先向右平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
C.先向右平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
D.先向左平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com