
【题目】已知![]() 是函数
是函数![]() 的切线,则
的切线,则![]() 的最小值为______.
的最小值为______.
【答案】![]()
【解析】
根据题意,设切线的坐标为(m,lnm+m),求出函数f(x)的导数,由导数的几何意义可得切线的方程,分析可得k![]() 1,b=lnm﹣1,代入化简得到lnm
1,b=lnm﹣1,代入化简得到lnm![]() 1,设g(m)=lnm
1,设g(m)=lnm![]() 1,求出g′(m),利用函数的导数与单调性的关系,分析可得g(m)的最小值,即可得答案.
1,求出g′(m),利用函数的导数与单调性的关系,分析可得g(m)的最小值,即可得答案.
根据题意,直线y=kx+b与函数f(x)=lnx+x相切,设切点为(m,lnm+m),
函数f(x)=lnx+x,其导数f′(x)![]() 1,则f′(m)
1,则f′(m)![]() 1,
1,
则切线的方程为:y﹣(lnm+m)=(![]() 1)(x﹣m),变形可得y=(
1)(x﹣m),变形可得y=(![]() 1)x+lnm﹣1,
1)x+lnm﹣1,
又由切线的方程为y=kx+b,
则k![]() 1,b=lnm﹣1,
1,b=lnm﹣1,
则2k+b![]() 2+lnm﹣1=lnm
2+lnm﹣1=lnm![]() 1,
1,
设g(m)=lnm![]() 1,其导数g′(m)
1,其导数g′(m)![]() ,
,
在区间(0,2)上,g′(m)<0,则g(m)=lnm![]() 1为减函数,
1为减函数,
在(2,+∞)上,g′(m)>0,则g(m)=lnm![]() 1为增函数,
1为增函数,
则g(m)min=g(2)=ln2+2,即2k+b的最小值为ln2+2;
故答案为:ln2+2.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】某公司生产一种化工产品,该产品若以每吨10万元的价格销售,每年可售出1000吨,若将该产品每吨分价格上涨![]() ,则每年的销售数量将减少
,则每年的销售数量将减少![]() ,其中m为正常数,销售的总金额为y万元.
,其中m为正常数,销售的总金额为y万元.
(1)当![]() 时,该产品每吨的价格上涨百分之几,可使销售总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售总金额最大?
(2)当![]() 时,若能使销售总金额比涨价前增加,试设定m的取值范围.
时,若能使销售总金额比涨价前增加,试设定m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具公司制作木质的椅子和书桌两种家具,需要木工和漆工两道工序,已知木工平均6个小时做一把椅子,10个小时做一张书桌,该公司每月木工最多有6000个工作时;漆工平均4个小时漆一把椅子,2个小时漆一张书桌,该公司每月漆工最多有2600个工作时![]() 又已知制作一把椅子和一张书桌的利润分别是15元和20元,根据以上条件,怎样安排每月的生产,才能获得最大的利润?
又已知制作一把椅子和一张书桌的利润分别是15元和20元,根据以上条件,怎样安排每月的生产,才能获得最大的利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构为了了解各年龄层对高考改革方案的关注程度,随机选取了200名年龄在![]() 内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为
内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
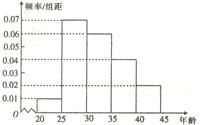
(1)求选取的市民年龄在![]() 内的人数;
内的人数;
(2)若从第3,4组用分层抽样的方法选取5名市民进行座谈,再从中选取2人在座谈会中作重点发言,求作重点发言的市民中至少有一人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() 的参数方程是
的参数方程是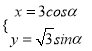 (
(![]() 为参数)以原点为极点,
为参数)以原点为极点, ![]() 轴正半轴为极轴,并取与直角坐标系相同的单位长度,建立极坐标系,曲线
轴正半轴为极轴,并取与直角坐标系相同的单位长度,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求曲线![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 、
、![]() 分别是曲线
分别是曲线![]() 和
和![]() 上的任意点,求
上的任意点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的各项都为正数,其前n项和为Sn,已知对任意n∈N*,Sn是![]() 和an的等差中项.
和an的等差中项.
(1)证明:数列{an}为等差数列;
(2)若bn=-n+5,求{an·bn}的最大项的值并求出取最大值时n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在高为6的等腰梯形![]() 中,
中, ![]() ,且
,且![]() ,
, ![]() ,将它沿对称轴
,将它沿对称轴![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .如图2,点
.如图2,点![]() 为
为![]() 中点,点
中点,点![]() 在线段
在线段![]() 上(不同于
上(不同于![]() ,
, ![]() 两点),连接
两点),连接![]() 并延长至点
并延长至点![]() ,使
,使![]() .
.

(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com