
 如图,在四棱锥S-ABCD中,SA=AB=2,SB=SD=2
如图,在四棱锥S-ABCD中,SA=AB=2,SB=SD=2| 2 |
| 2 |
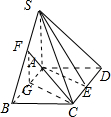 ∴SA⊥AB,SA⊥AD;
∴SA⊥AB,SA⊥AD;

 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
| n(an-a1) |
| 2 |
| Sn+2 |
| Sn+1 |
| Sn+1 |
| Sn+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| |PT| |
| |MN| |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 偏瘦 | 正常 | 偏胖 | |
| 女生(人) | x | 120 | y |
| 男生(人) | 50 | 180 | z |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,设F是抛物线E:x2=2py(p>0)的焦点,过点F作斜率分别为k1、k2的两条直线l1、l2,且k1•k2=-1,l1与E相交于点A、B,l2与E相交于点C,D.已知△AFO外接圆的圆心到抛物线的准线的距离为3(O为坐标原点).
如图所示,设F是抛物线E:x2=2py(p>0)的焦点,过点F作斜率分别为k1、k2的两条直线l1、l2,且k1•k2=-1,l1与E相交于点A、B,l2与E相交于点C,D.已知△AFO外接圆的圆心到抛物线的准线的距离为3(O为坐标原点).| AF |
| FB |
| DF |
| FC |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+1+an+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com