
ЗжЮі ИљОнЬтвтЕУЕН$\overrightarrow{OA}$+$\overrightarrow{OB}$=2$\overrightarrow{a}$ЃЌЕУЕНШ§НЧаЮOABЕФИпКЭБпГЄЃЌИљОнУцЛ§ЙЋЪНМЦЫуМДПЩЃЎ
НтД№ НтЃКЯђСП$\overrightarrow{a}$=ЃЈ-$\frac{1}{2}$ЃЌ$\frac{\sqrt{3}}{2}$ЃЉЃЌПЩЕУ|$\overrightarrow{a}$|=1ЃЌ
Ёп$\overrightarrow{OA}$=$\overrightarrow{a}$-$\overrightarrow{b}$ЃЌ$\overrightarrow{OB}$=$\overrightarrow{a}$+$\overrightarrow{b}$ЃЌ
ЁїOABЪЧЕШБпШ§НЧаЮЃЌ
ПЩЕУ$\overrightarrow{OA}$+$\overrightarrow{OB}$=2$\overrightarrow{a}$ЃЌ
МДга$\frac{1}{2}$|$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{a}$|=1ЃЌ
дђШ§НЧаЮOABЕФИпЮЊ1ЃЌБпГЄЮЊ$\frac{2\sqrt{3}}{3}$ЃЌ
дђOABЕФУцЛ§ЮЊ$\frac{\sqrt{3}}{4}$ЁСЃЈ$\frac{2\sqrt{3}}{3}$ЃЉ2=$\frac{\sqrt{3}}{3}$ЃЎ
ЙЪД№АИЮЊЃК$\frac{\sqrt{3}}{3}$ЃЎ
ЕуЦР БОЬтПМВщСЫЦНУцЯђСПЕФЪ§СПЛ§ЙЋЪНЁЂЯђСПЪ§СПЛ§ЕФдЫЫуаджЪКЭФЃЕФЙЋЪНКЭШ§НЧаЮЕФУцЛ§ЧѓЗЈЕШжЊЪЖЃЌЪєгкжаЕЕЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 2x-y+1=0 | BЃЎ | x-2y+1=0 | CЃЎ | 2x-y-1=0 | DЃЎ | x-2y-1=0 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
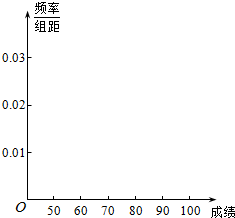 ФГаЃИпЖўФъМЖЕФ600УћбЇЩњВЮМгвЛДЮПЦЦежЊЪЖОКШќЃЌШЛКѓЫцЛњГщШЁ50УћбЇЩњЕФГЩМЈНјааЭГМЦЗжЮіЃЎ
ФГаЃИпЖўФъМЖЕФ600УћбЇЩњВЮМгвЛДЮПЦЦежЊЪЖОКШќЃЌШЛКѓЫцЛњГщШЁ50УћбЇЩњЕФГЩМЈНјааЭГМЦЗжЮіЃЎ| Зж зщ | ЦЕЪ§ | ЦЕТЪ | ЦЕТЪ/зщОр |
| [50ЃЌ60ЃЉ | 5 | ||
| [60ЃЌ70ЃЉ | 10 | ||
| [70ЃЌ80ЃЉ | 15 | ||
| [80ЃЌ90ЃЉ | 15 | ||
| [90ЃЌ100ЃЉ | 5 | ||
| КЯ МЦ | 50 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ЖдШЮвтxЁЪRЃЌЖМгаx2ЃМln2 | BЃЎ | ВЛДцдкx0=RЃЌЪЙЕУ ${{x}_{0}}^{2}$ЃМln2 | ||
| CЃЎ | Дцдкx0=RЃЌЪЙЕУ ${{x}_{0}}^{2}$Ёнln2 | DЃЎ | Дцдкx0=RЃЌЪЙЕУ ${{x}_{0}}^{2}$Ёмln2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ЃЈ-3ЃЌ-2ЃЉ | BЃЎ | ЃЈ-1ЃЌ0ЃЉ | CЃЎ | ЃЈ0ЃЌ1ЃЉ | DЃЎ | ЃЈ4ЃЌ5ЃЉ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com