
分析 由条件利用正弦定理、二倍角的正弦公式求得$\frac{b}{a}$=2cosA,再分B为钝角、C为钝角两种情况,分别求得A的范围,可得$\frac{b}{a}$的取值范围.
解答 解:钝角△ABC中,∵B=2A,则$\frac{b}{a}$=$\frac{sinB}{sinA}$=$\frac{sin2A}{sinA}$=$\frac{2sinAcosA}{sinA}$=2cosA.
若B为钝角,即 $\frac{π}{2}$<2A<π,即$\frac{π}{4}$<A<$\frac{π}{2}$,∴0<cosA<$\frac{\sqrt{2}}{2}$,∴$\frac{b}{a}$∈(0,$\sqrt{2}$).
若C=π-A-B=π-3A为钝角,则$\frac{π}{2}$<π-3A<π,∴0<A<$\frac{π}{6}$,$\frac{\sqrt{3}}{2}$<cosA<1,∴$\frac{b}{a}$∈($\frac{\sqrt{3}}{2}$,1).
综上可得,$\frac{b}{a}$的取值范围是(0,$\sqrt{2}$)∪($\frac{\sqrt{3}}{2}$,1),
故答案为:(0,$\sqrt{2}$)∪($\frac{\sqrt{3}}{2}$,1).
点评 本题主要考查二倍角的正弦公式、正弦定理的应用,余弦函数的定义域和值域,体现了分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),点(-1,$\frac{\sqrt{2}}{2}$)在椭圆C上,点T满足$\overrightarrow{OT}$=$\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$•$\overrightarrow{OF}$(其中O为坐标原点),过点F作一斜率为1的直线交椭圆于P、Q两点(其中P点在x轴上方,Q点在x轴下方)
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),点(-1,$\frac{\sqrt{2}}{2}$)在椭圆C上,点T满足$\overrightarrow{OT}$=$\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$•$\overrightarrow{OF}$(其中O为坐标原点),过点F作一斜率为1的直线交椭圆于P、Q两点(其中P点在x轴上方,Q点在x轴下方)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 周期为2π的奇函数 | B. | 周期为2π的偶函数 | ||
| C. | 周期为π的奇函数 | D. | 周期为π的偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组数 | 分组 | 频数 | 频率 | “光盘族”占本组比例 |
| 第1组 | [25,30) | 50 | 0.05 | 30% |
| 第2组 | [30,35) | 100 | 0.10 | 30% |
| 第3组 | [35,40) | 150 | 0.15 | 40% |
| 第4组 | [40,45) | 200 | 0.20 | 50% |
| 第5组 | [45,50) | a | b | 65% |
| 第6组 | [50,55) | 200 | 0.20 | 60% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
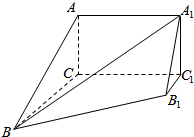 如图,几何体ABC-A1B1C1中,平面ABC∥平面A1B1C1,平面ACC1A1为矩形,平面ACC1A1⊥平面BCC1B1,已知AC=3,BC=AA1=4,BB1=5,B1C1=1
如图,几何体ABC-A1B1C1中,平面ABC∥平面A1B1C1,平面ACC1A1为矩形,平面ACC1A1⊥平面BCC1B1,已知AC=3,BC=AA1=4,BB1=5,B1C1=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com