
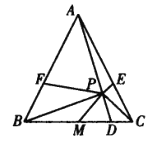
【题目】如图,在△ABC中,AB=AC,M是BC的中点,D、E、F分别是边BC、CA、AB上的点,且AE=AF,△AEF的外接圆交线段AD于点P.若点P满足![]() ,证明:
,证明:![]() .
.
【答案】见解析
【解析】
在△AEF的外接圆中,由于AE=AF,
故![]() .
.
因此,P、D、B、F与P、D、C、E分别四点共圆.
于是,![]() .
.
如图,设P在边BC、CA、AB上的射影分别为![]() 、
、![]() 、
、![]() .则△
.则△![]() .
.
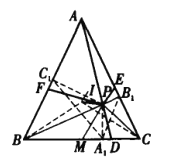
由![]() ,得
,得
![]() .①
.①
设△ABC的内心为I,下证:B、I、P、C四点共圆.
联结![]() .因
.因![]() 和
和![]() 分别四点共圆,
分别四点共圆,
则![]() .
.
又由式①,有![]() .
.
所以,![]() .
.
因此,![]() ..
..
而![]() ,
,![]() ,
,
所以,![]()
又![]() ,
,
![]() ,
,![]() .
.
故![]() .
.
因此,B、I、P、C四点共圆.
于是,![]() .
.
如图,延长AM交△ABC的外接圆于点O,则AO为外接圆的直径.于是,OB⊥AB,OC⊥AC,且OB=OI=OC.
因此,点O是点B、I、P、C所在圆的圆心.
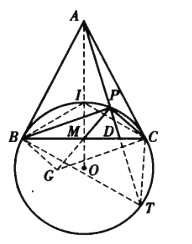
从而,AB、AC为![]() 的切线.
的切线.
延长AD交![]() 于点T,则
于点T,则![]() .
.
所以,![]() .
.
又由![]() ,得
,得![]() .
.
因AB=AC,故
![]() .②
.②
延长PM到点G,使GM=PM,则四边形BPCG为平行四边形有
![]() .③
.③
由式②得![]() .④
.④
由式③、④得![]() .
.
所以,![]() ,即
,即
![]() .
.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:
【题目】数列{an}满足an+1+(-1)n an =2n-1,则{an}的前64项和为( )
A. 4290 B. 4160 C. 2145 D. 2080
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】男生4人和女生3人排成一排拍照留念.
(1)有多少种不同的排法(结果用数值表示)?
(2)要求两端都不排女生,有多少种不同的排法(结果用数值表示)?
(3)求甲乙两人相邻的概率.(结果用最简分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与椭圆
与椭圆![]() 有一个相同的焦点,过点
有一个相同的焦点,过点![]() 且与
且与![]() 轴不垂直的直线
轴不垂直的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)试问直线![]() 是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甜皮鸭,乐山人称卤鸭子,也称嘉州甜皮鸭,是乐山著名美食,起源于乐山市夹江县木城古镇,每年吸引成千上万的外地人前来品尝.某商家生产卤鸭子,每公斤鸭子的成本为![]() 元,加工费为
元,加工费为![]() 元(
元(![]() 为常数),且
为常数),且![]() ,设该商家每公斤卤鸭子的售价为
,设该商家每公斤卤鸭子的售价为![]() 元(
元(![]() ),日销售量
),日销售量![]() (单位:公斤),且
(单位:公斤),且![]() (
(![]() 为自然对数的底数).根据市场调查,当每公斤卤鸭子的出售价为
为自然对数的底数).根据市场调查,当每公斤卤鸭子的出售价为![]() 元时,日销售量为
元时,日销售量为![]() 公斤.
公斤.
(1)求该商家的每日利润![]() 元与每公斤卤鸭子的出售价
元与每公斤卤鸭子的出售价![]() 元的函数关系式;
元的函数关系式;
(2)若![]() ,当每公斤卤鸭子的出售价
,当每公斤卤鸭子的出售价![]() 为多少元时,该商家的利润
为多少元时,该商家的利润![]() 最大,并求出利润的最大值.
最大,并求出利润的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点为极点,
为参数).以原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)若曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 在第一象限的交点为
在第一象限的交点为![]() ,与
,与![]() 的交点为
的交点为![]() (异于原点),求
(异于原点),求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是正方体的平面展开图,在这个正方体中,正确的命题是( )

A. BD与CF成60°角 B. BD与EF成60°角 C. AB与CD成60°角 D. AB与EF成60°角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com