
【题目】已知函数![]() (
(![]() ,
,![]() 是自然对数的底数).
是自然对数的底数).
(1)若函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,试确定函数
,试确定函数![]() 的单调区间;
的单调区间;
(2)①当![]() ,
,![]() 时,若对于任意
时,若对于任意![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的最小值;②当
的最小值;②当![]() 时,设函数
时,设函数![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1)![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;(2)①
上单调递增;(2)①![]() ;②存在
;②存在![]() ,使得命题成立
,使得命题成立
【解析】
(1)利用切线方程可知![]() ,
,![]() ,从而构造出方程组求得
,从而构造出方程组求得![]() ,得到
,得到![]() 解析式,根据导函数的符号确定
解析式,根据导函数的符号确定![]() 的单调区间;(2)①将问题转化为
的单调区间;(2)①将问题转化为![]() 对任意
对任意![]() 恒成立;设
恒成立;设![]() ,利用导数求解
,利用导数求解![]() ,可得
,可得![]() ;②设存在
;②设存在![]() ,使得
,使得![]() ,将问题转化为
,将问题转化为![]() ,利用导数分别在
,利用导数分别在![]() ,
,![]() 和
和![]() 研究
研究![]() 的最大值和最小值,从而根据最值的关系可求得
的最大值和最小值,从而根据最值的关系可求得![]() 的取值范围.
的取值范围.
(1)由题意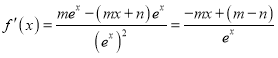
![]() 在点
在点![]() 处的切线方程为:
处的切线方程为:![]()
![]() ,
,![]() ,即:
,即: 解得:
解得:![]() ,
,![]()
![]() ,
,![]()
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
(2)①由![]() ,
,![]() ,
,![]() ,即:
,即:![]()
对任意![]() ,都有
,都有![]() 恒成立等价于
恒成立等价于![]() 对任意
对任意![]() 恒成立
恒成立
记![]() ,
,![]()
设![]()
![]() 对
对![]() 恒成立
恒成立
![]() 在
在![]() 单调递增
单调递增
而![]() ,
,![]()
![]() 在
在![]() 上有唯一零点
上有唯一零点![]()
当 时,
时,![]() ,当
,当![]() 时,
时,![]()
![]() 在
在![]() 单调递减,在
单调递减,在![]() 上单调递增
上单调递增
![]() 的最大值是
的最大值是![]() 和
和![]() 中的较大的一个
中的较大的一个
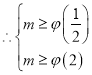 ,即
,即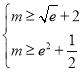
![]() ,
,
![]() 的最小值为
的最小值为![]()
②假设存在![]() ,使得
,使得![]() ,则问题等价于
,则问题等价于![]()
![]()
![]()
⑴当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减
上单调递减
![]() ,即
,即![]() ,得:
,得:![]()
![]()
(2)当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增
上单调递增
![]() ,即
,即![]() ,得:
,得:![]()
![]()
(3)当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
![]() ,即
,即![]() ……(*)
……(*)
由(1)知![]()
![]() 上单调递减,故
上单调递减,故![]() ,而
,而![]()
![]() 不等式(*)无解
不等式(*)无解
综上所述,存在![]() ,使得命题成立
,使得命题成立


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:高中数学 来源: 题型:
【题目】一年之计在于春,一日之计在于晨,春天是播种的季节,是希望的开端.某种植户对一块地的![]() 个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为
个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为![]() ,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.
,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.
(1)当![]() 取何值时,有3个坑要补播种的概率最大?最大概率为多少?
取何值时,有3个坑要补播种的概率最大?最大概率为多少?
(2)当![]() 时,用
时,用![]() 表示要补播种的坑的个数,求
表示要补播种的坑的个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,
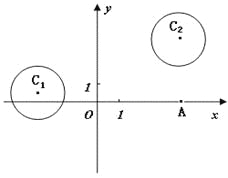
已知圆![]() 和圆
和圆![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,
,
求直线![]() 的方程;(2)设P为平面上的点,满足:
的方程;(2)设P为平面上的点,满足:
存在过点P的无穷多对互相垂直的直线![]() 和
和![]() ,
,
它们分别与圆![]() 和圆
和圆![]() 相交,且直线
相交,且直线![]() 被圆
被圆![]()
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查煤矿公司员工的饮食习惯与月收入之间的关系,随机抽取了30名员工,并制作了这30人的月平均收入的频率分布直方图和饮食指数表(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主).其中月收入4000元以上员工中有11人饮食指数高于70.
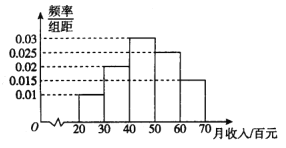
20 | 21 | 21 | 25 | 32 | 33 |
36 | 37 | 42 | 43 | 44 | 45 |
45 | 58 | 58 | 59 | 61 | 66 |
74 | 75 | 76 | 77 | 77 | 78 |
78 | 82 | 83 | 85 | 86 | 90 |
(Ⅰ)是否有95%的把握认为饮食习惯与月收入有关系?若有请说明理由,若没有,说明理由并分析原因;
(Ⅱ)以样本中的频率作为概率,从该公司所有主食蔬菜的员工中随机抽取3人,这3人中月收入4000元以上的人数为![]() ,求
,求![]() 的分布列与期望;
的分布列与期望;
(Ⅲ)经调查该煤矿公司若干户家庭的年收入![]() (万元)和年饮食支出
(万元)和年饮食支出![]() (万元)具有线性相关关系,并得到
(万元)具有线性相关关系,并得到![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:![]() .若该公司一个员工与其妻子的月收入恰好都为这30人的月平均收入(该家庭只有两人收入),估计该家庭的年饮食支出费用.
.若该公司一个员工与其妻子的月收入恰好都为这30人的月平均收入(该家庭只有两人收入),估计该家庭的年饮食支出费用.
附:
![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是半圆
是半圆![]() 的直径,
的直径,![]() ,
,![]() 是将半圆圆周四等分的三个分点.
是将半圆圆周四等分的三个分点.

(1)从![]() 这5个点中任取3个点,求这3个点组成直角三角形的概率;
这5个点中任取3个点,求这3个点组成直角三角形的概率;
(2)在半圆内任取一点![]() ,求
,求![]() 的面积大于
的面积大于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,![]() ,四边形BDEF是矩形,平面
,四边形BDEF是矩形,平面![]() 平面ABCD,
平面ABCD,![]() ,H是CF的中点.
,H是CF的中点.

(1)求证:![]() 平面BDEF;
平面BDEF;
(2)求直线DH与平面CEF所成角的正弦值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com