练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，已知是半圆的直径，，是将半圆圆周四等分的三个分点．

    （1）从这5个点中任取3个点，求这3个点组成直角三角形的概率；

    （2）在半圆内任取一点，求的面积大于的概率．

    【答案】（1）；（2）.

    【解析】

    试题分析：对于问题（1）首先求出从个点中任取个点，一共可以组成的三角形的个数，再求出以为直径的三角形的个数，即可求出所求的概率；对于问题（2）首先求出当三角形的面积等于时点在半圆内的位置，然后再根据几何概型即可求得所需的结论.

    试题解析：（1）从这个点中任取个点，一共可以组成个三角形：，其中是直角三角形的只有个，所以组成直角三角形的概率为．

    （2）连接，取线段的中点，则，

    易求得，当点在线段上时，，

    所以只有当点落在阴影部分时，面积才能大于，而，所以由几何概型的概率公式得的面积大于的概率为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某公司研发了两种具有自主知识产权的操作系统，分别命名为“天下”、“东方”.这两套操作系统均适用于手机、电脑、车联网、物联网等，且较国际同类操作系统更加流畅.

    （1）为了解喜欢“天下”系统是否与性别有关，随机调查了名男用户和名女用户，每位用户对“天下”系统给出喜欢或不喜欢的评价，得到下面列联表：

    请问：能否有的把握认为男、女用户对“天下”系统的喜欢有差异？

    附：.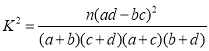

    （2）该公司选定万名用户对“天下”和“东方”操作系统（以下简称“天下”、“东方”）进行测试，每个用户只能从“天下”或“东方”中选择一个使用，每经过一个月后就给用户一次重新选择“天下”或“东方”的机会.这个月选择“天下”的用户在下个月选择“天下”的概率均为，选择“东方”的概率均为，；这个月选择“东方”的用户在下个月选择“天下”的概率均为，选择“东方”的概率均为，.记表示第个月用户选择“天下”的概率，已知，，，，.

    （ⅰ）求的值；

    （ⅱ）证明：数列（）为等比数列；

    （ⅲ）预测选择“天下”操作系统的用户数量不超过多少万人.（精确到1万）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某商品每件的生产成本（元）与销售价格（元）具有线性相关关系，对应数据如表所示：

    （元）

    5

    6

    7

    8

    （元）

    15

    17

    21

    27

    （1）求出关于的线性回归方程；

    （2）若该商品的月销售量（千件）与生产成本（元）的关系为，，根据（1）中求出的线性回归方程，预测当为何值时，该商品的月销售额最大．

    附：，.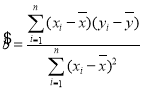

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（，是自然对数的底数）.

    （1）若函数在点处的切线方程为，试确定函数的单调区间；

    （2）①当，时，若对于任意，都有恒成立，求实数的最小值；②当时，设函数，是否存在实数，使得？若存在，求出的取值范围；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知分别是双曲线E： 的左、右焦点，P是双曲线上一点， 到左顶点的距离等于它到渐近线距离的2倍，（1）求双曲线的渐近线方程；（2）当时， 的面积为，求此双曲线的方程。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，其中，是自然对数的底数.

    （1）若在上存在两个极值点，求的取值范围；

    （2）若，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆，是长轴的一个端点，弦过椭圆的中心，点在第一象限，且，．

    （1）求椭圆的标准方程；

    （2）设、为椭圆上不重合的两点且异于、，若的平分线总是垂直于轴，问是否存在实数，使得？若不存在，请说明理由；若存在，求取得最大值时的的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线：的焦点为，直线与抛物线交于，两点，是坐标原点．

    （1）若直线过点且，求直线的方程；

    （2）已知点，若直线不与坐标轴垂直，且，证明：直线过定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某隧道的剖面图是由半圆及矩形组成，交通部门拟在隧道顶部安装通风设备（视作点），为了固定该设备，计划除从隧道最高点处使用钢管垂直向下吊装以外，再在两侧自两点分别使用钢管支撑.已知道路宽，设备要求安装在半圆内部，所使用的钢管总长度为.

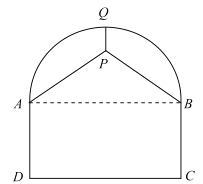
    （1）①设，将表示为关于的函数；

    ②设，将表示为关于的函数；

    （2）请选用（1）中的一个函数关系式，说明如何设计，所用的钢管材料最省？

    查看答案和解析>>

    同步练习册答案