
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 是坐标原点.
是坐标原点.
(1)若直线![]() 过点
过点![]() 且
且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)已知点![]() ,若直线
,若直线![]() 不与坐标轴垂直,且
不与坐标轴垂直,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)法一:焦点![]() ,当直线
,当直线![]() 斜率不存在时,方程为
斜率不存在时,方程为![]() ,说明不符合题意,故直线的斜率存在,设直线
,说明不符合题意,故直线的斜率存在,设直线![]() 方程为
方程为![]() 与
与![]() 联立得
联立得![]() ,利用韦达定理转化求解
,利用韦达定理转化求解![]() ,求解直线方程.
,求解直线方程.
法二:焦点![]() ,显然直线
,显然直线![]() 不垂直于
不垂直于![]() 轴,设直线
轴,设直线![]() 方程为
方程为![]() ,与
,与![]() 联立得
联立得![]() ,设
,设![]() ,
,![]() ,利用韦达定理以及距离公式,转化求解即可.
,利用韦达定理以及距离公式,转化求解即可.
(2)设![]() ,
,![]() ,设直线
,设直线![]() 方程为
方程为![]() 与
与![]() 联立得:
联立得:![]() ,通过韦达定理以及斜率关系,求出直线系方程,即可推出结果.
,通过韦达定理以及斜率关系,求出直线系方程,即可推出结果.
解:(1)法一:焦点![]() ,
,
当直线![]() 斜率不存在时,方程为
斜率不存在时,方程为![]() ,与抛物线的交点坐标分别为
,与抛物线的交点坐标分别为![]() ,
,![]() ,
,
此时![]() ,不符合题意,故直线的斜率存在.
,不符合题意,故直线的斜率存在.
设直线![]() 方程为
方程为![]() 与
与![]() 联立得
联立得![]() ,
,
当![]() 时,方程只有一根,不符合题意,故
时,方程只有一根,不符合题意,故![]() .
.![]() ,
,
抛物线的准线方程为![]() ,
,
由抛物线的定义得![]()
![]() ,
,
解得![]() ,
,
所以![]() 方程为
方程为![]() 或
或![]() .
.
法二:焦点![]() ,显然直线
,显然直线![]() 不垂直于
不垂直于![]() 轴,设直线
轴,设直线![]() 方程为
方程为![]() ,
,
与![]() 联立得
联立得![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
![]() ,
,
由![]() ,解得
,解得![]() ,
,
所以![]() 方程为
方程为![]() 或
或![]() .
.
(2)设![]() ,
,![]() ,
,
设直线![]() 方程为
方程为![]() 与
与![]() 联立得:
联立得:![]() ,
,
可得![]() ,
,![]() .
.
由![]() 得
得![]() ,即
,即![]() .
.
整理得![]() ,即
,即![]() ,
,
整理得![]() ,
,
即![]() ,即
,即![]() .
.
故直线![]() 方程为
方程为![]() 过定点
过定点![]() .
.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,
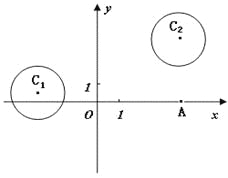
已知圆![]() 和圆
和圆![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,
,
求直线![]() 的方程;(2)设P为平面上的点,满足:
的方程;(2)设P为平面上的点,满足:
存在过点P的无穷多对互相垂直的直线![]() 和
和![]() ,
,
它们分别与圆![]() 和圆
和圆![]() 相交,且直线
相交,且直线![]() 被圆
被圆![]()
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是半圆
是半圆![]() 的直径,
的直径,![]() ,
,![]() 是将半圆圆周四等分的三个分点.
是将半圆圆周四等分的三个分点.

(1)从![]() 这5个点中任取3个点,求这3个点组成直角三角形的概率;
这5个点中任取3个点,求这3个点组成直角三角形的概率;
(2)在半圆内任取一点![]() ,求
,求![]() 的面积大于
的面积大于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于40分钟的观众称为体育迷.若抽取100人中有女性55人,其中女体育迷有10人,完成答题卡中的列联表并判断能否在犯错误概率不超过0.05的前提下认为体育迷与性别有关系?
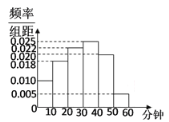
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
附表及公式: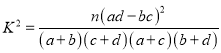 ,
,![]() .
.
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (a,b
(a,b![]() R)的导函数为
R)的导函数为![]() ,已知
,已知![]() ,
,![]() 是
是![]() 的两个不同的零点.
的两个不同的零点.
(1)证明:![]() ;
;
(2)当b=0时,若对任意x>0,不等式![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(3)求关于x的方程![]() 的实根的个数.
的实根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,![]() ,四边形BDEF是矩形,平面
,四边形BDEF是矩形,平面![]() 平面ABCD,
平面ABCD,![]() ,H是CF的中点.
,H是CF的中点.

(1)求证:![]() 平面BDEF;
平面BDEF;
(2)求直线DH与平面CEF所成角的正弦值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com