
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,
,![]() 平面
平面![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
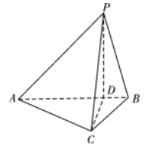
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值。
的平面角的余弦值。
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)先由线面垂直的判定定理,证明![]() 平面
平面![]() ,进而可得平面
,进而可得平面![]() 平面
平面![]() ;
;
(2)以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系,求出平面
轴,建立空间直角坐标系,求出平面![]() 与平面
与平面![]() 的一个法向量,根据向量夹角公式,求出两向量夹角的余弦值,进而可得出结果.
的一个法向量,根据向量夹角公式,求出两向量夹角的余弦值,进而可得出结果.
(1)因为![]() ,
,![]() ,
,
所以![]()
所以![]() 是直角三角形,
是直角三角形,![]() ;
;
在![]() 中,由
中,由![]() ,
,![]() ,
,
不妨设![]() ,由
,由![]() 得,
得,![]() ,
,![]() ,
,![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得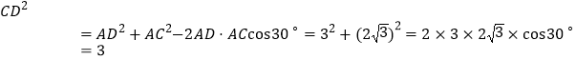 ,
,
故![]() ,
,
所以![]() ,所以
,所以![]() ;
;
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ;
;
(2)因为![]() 平面
平面![]() ,所以
,所以![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,即
,即![]() ,
,
可得![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,

由(1)得![]() ,以
,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 所在直线为
所在直线为![]() 轴,建立如图所示的空间直角坐标系,则
轴,建立如图所示的空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() 为平面
为平面![]() 的一个法向量。
的一个法向量。
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
因为![]() ,
,![]() ,
,
则由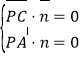 得
得![]()
令![]() ,则
,则![]() ,
,![]() ,
,
则![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
故![]()
故二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .以极点为原点,极轴为
.以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为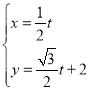 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求直线![]() 被曲线
被曲线![]() 所截得的弦长.
所截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一![]() 班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.

![]() 1
1![]() 求分数在
求分数在![]() 的频数及全班人数;
的频数及全班人数;
![]() 2
2![]() 求分数在
求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
![]() 3
3![]() 若要从分数在
若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某商品每件的生产成本![]() (元)与销售价格
(元)与销售价格![]() (元)具有线性相关关系,对应数据如表所示:
(元)具有线性相关关系,对应数据如表所示:
| 5 | 6 | 7 | 8 |
| 15 | 17 | 21 | 27 |
(1)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该商品的月销售量![]() (千件)与生产成本
(千件)与生产成本![]() (元)的关系为
(元)的关系为![]() ,
,![]() ,根据(1)中求出的线性回归方程,预测当
,根据(1)中求出的线性回归方程,预测当![]() 为何值时,该商品的月销售额最大.
为何值时,该商品的月销售额最大.
附: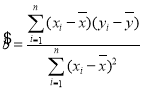 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据新高考改革方案,某地高考由文理分科考试变为“3+3”模式考试.某学校为了解高一年425名学生选课情况,在高一年下学期进行模拟选课,统计得到选课组合排名前4种如下表所示,其中物理、化学、生物为理科,政治、历史、地理为文科,“√”表示选择该科,“×”表示未选择该科,根据统计数据,下列判断错误的是
学科 人数 | 物理 | 化学 | 生物 | 政治 | 历史 | 地理 |
124 | √ | √ | × | × | × | √ |
101 | × | × | √ | × | √ | √ |
86 | × | √ | √ | × | × | √ |
74 | √ | × | √ | × | √ | × |
A. 前4种组合中,选择生物学科的学生更倾向选择两理一文组合
B. 前4种组合中,选择两理一文的人数多于选择两文一理的人数
C. 整个高一年段,选择地理学科的人数多于选择其他任一学科的人数
D. 整个高一年段,选择物理学科的人数多于选择生物学科的人数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 是自然对数的底数).
是自然对数的底数).
(1)若函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,试确定函数
,试确定函数![]() 的单调区间;
的单调区间;
(2)①当![]() ,
,![]() 时,若对于任意
时,若对于任意![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的最小值;②当
的最小值;②当![]() 时,设函数
时,设函数![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知F是抛物线C:![]() 的焦点,过E(﹣l,0)的直线
的焦点,过E(﹣l,0)的直线![]() 与抛物线分別交于A,B两点(点A,B在x轴的上方).
与抛物线分別交于A,B两点(点A,B在x轴的上方).
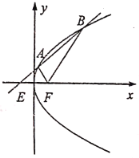
(1)设直线AF,BF的斜率分別为![]() ,
,![]() ,证明:
,证明:![]() ;
;
(2)若![]() ABF的面积为4,求直线
ABF的面积为4,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com