
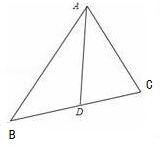
 已知AD是△ABC的角平分线,且AC=2,AB=4,cos∠BAC=$\frac{11}{16}$.
已知AD是△ABC的角平分线,且AC=2,AB=4,cos∠BAC=$\frac{11}{16}$.分析 (1)由cos∠BAC=$\frac{11}{16}$,∠BAC∈(0,π),可得sin∠BAC=$\sqrt{1-co{s}^{2}∠BAC}$,即可得出S△ABC.
(2)由AD是△ABC的角平分线,可得$\frac{BD}{DC}$=$\frac{AB}{AC}$=2,∠BAD=$\frac{1}{2}$∠BAC,利用cos∠BAC=1-2sin2∠BAD,解得sin∠BAD.利用S△ABD=$\frac{1}{3}$S△ABC=$\frac{\sqrt{15}}{4}$=$\frac{1}{2}AB×ADsin\frac{1}{2}∠BAC$,即可得出.
解答 解:(1)∵cos∠BAC=$\frac{11}{16}$,∠BAC∈(0,π),∴sin∠BAC=$\sqrt{1-co{s}^{2}∠BAC}$=$\frac{3\sqrt{15}}{16}$.
∴S△ABC=$\frac{1}{2}$×2×4×$\frac{3\sqrt{15}}{16}$=$\frac{3\sqrt{15}}{4}$.
(2)由AD是△ABC的角平分线,∴$\frac{BD}{DC}$=$\frac{AB}{AC}$=2,∠BAD=$\frac{1}{2}$∠BAC,
∴cos∠BAC=1-2sin2∠BAD,∴$\frac{11}{16}$=1-2sin2∠BAD,解得sin∠BAD=$\frac{\sqrt{10}}{8}$.
∴S△ABD=$\frac{2}{3}$S△ABC=$\frac{\sqrt{15}}{2}$=$\frac{1}{2}AB×ADsin\frac{1}{2}∠BAC$=$\frac{1}{2}×4×AD$×$\frac{\sqrt{10}}{8}$.
解得AD=$\sqrt{6}$.
点评 本题考查了角平分线的性质、三角形面积计算公式、倍角公式、三角函数求值,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题

| A. | -1,4 | B. | 3,$\frac{1}{2}$ | C. | $\frac{1}{2},-\frac{5}{4}$ | D. | 3,$-\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 商店名称 | A | B | C | D | E |
| 销售额x (千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y (百万元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
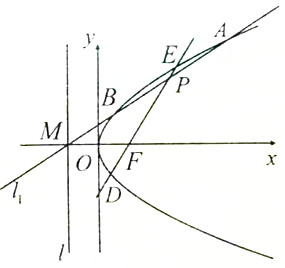 已知抛物线C:y2=2px(p>0)的焦点F与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右焦点重合,抛物线C的准线l与x轴的交点为M,过点M且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF与抛物线C交于D,E两点
已知抛物线C:y2=2px(p>0)的焦点F与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右焦点重合,抛物线C的准线l与x轴的交点为M,过点M且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF与抛物线C交于D,E两点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com