
分析 利用复数代数形式的乘除运算化简$\frac{\sqrt{2}i}{1+i}$,再进一步求出$\frac{\sqrt{2}i}{1+i}$的平方,则答案可求.
解答 解:$\frac{\sqrt{2}i}{1+i}=\frac{\sqrt{2}i(1-i)}{(1+i)(1-i)}=\frac{\sqrt{2}+\sqrt{2}i}{2}$,
$(\frac{\sqrt{2}i}{1+i})^{2}=(\frac{\sqrt{2}+\sqrt{2}i}{2})^{2}=\frac{4i}{4}=i$,
则${(\frac{{\sqrt{2}i}}{1+i})^{100}}$=i50=(i2)25=-1.
故答案为:-1.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.


科目:高中数学 来源: 题型:解答题
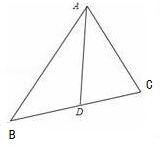 已知AD是△ABC的角平分线,且AC=2,AB=4,cos∠BAC=$\frac{11}{16}$.
已知AD是△ABC的角平分线,且AC=2,AB=4,cos∠BAC=$\frac{11}{16}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{2}{11}$ | C. | 2 | D. | $\frac{5}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
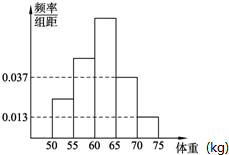 某省组织部为了了解今年全省高三毕业班准备报考飞行员的学生的体重情况,对该省某校高三毕业班准备报考飞行员的学生的体重进行了统计,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
某省组织部为了了解今年全省高三毕业班准备报考飞行员的学生的体重情况,对该省某校高三毕业班准备报考飞行员的学生的体重进行了统计,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{6}{5}$ | B. | $\frac{6}{5}$ | C. | -$\frac{8}{5}$ | D. | $\frac{8}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $C_n^{m-1}$ | B. | $A_n^{m-1}$ | C. | $C_n^m$ | D. | $A_n^m$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com