
分析 (1)把Vn=2n-1代入Vn=$\frac{{{a_1}+{a_2}+…+{a_n}}}{n}$,得到${a}_{1}+{a}_{2}+…+{a}_{n}=2{n}^{2}+n$,进一步得到${a}_{1}+{a}_{2}+…+{a}_{n-1}=2(n-1)^{2}+(n-1)$,两式作差可得数列{an}的通项公式;
(2)求出等比数列的通项公式并求得平均数为Vn,代入Vn>t-$\frac{1}{n}$,分离参数t后求得$\frac{{2}^{n}}{n}$的最小值得答案.
解答 解:(1)∵Vn=$\frac{{{a_1}+{a_2}+…+{a_n}}}{n}$,∴$\frac{{{a_1}+{a_2}+…+{a_n}}}{n}$=2n+1,
变形得${a}_{1}+{a}_{2}+…+{a}_{n}=2{n}^{2}+n$,①
当n≥2时,有${a}_{1}+{a}_{2}+…+{a}_{n-1}=2(n-1)^{2}+(n-1)$,②
①-②得an=4n-1(n≥2),
又当n=1时,V1=a1=2×1+1=3,适合an=4n-1,
故an=4n-1;
(2)∵数列{an}的首项为1,公比为2的等比数列,
∴${a}_{n}={2}^{n-1}$,其平均数${V}_{n}=\frac{{2}^{n}-1}{n}$,
由已知Vn>t-$\frac{1}{n}$对一切n∈N*恒成立,即$\frac{{2}^{n}-1}{n}>t-\frac{1}{n}$对一切n∈N*恒成立,
也就是t$<\frac{{2}^{n}}{n}$恒成立,令f(n)=$\frac{{2}^{n}}{n}$,则$\frac{f(n+1)}{f(n)}=\frac{2n}{n+1}=2-\frac{2}{n+1}$,
当n=1时,$\frac{f(n+1)}{f(n)}=1$,当n>1,n∈N*时,$\frac{f(n+1)}{f(n)}>1$,
∴f(n)≥f(1)=2.
因此实数t的范围是t<2.
点评 本题是数列与不等式的综合题,考查了等比数列的通项公式,考查了利用分离参数法求解恒成立问题,是中档题.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:解答题
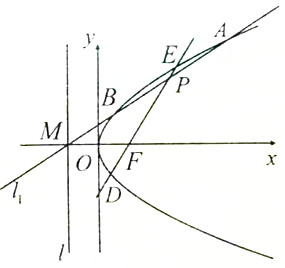 已知抛物线C:y2=2px(p>0)的焦点F与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右焦点重合,抛物线C的准线l与x轴的交点为M,过点M且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF与抛物线C交于D,E两点
已知抛物线C:y2=2px(p>0)的焦点F与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右焦点重合,抛物线C的准线l与x轴的交点为M,过点M且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF与抛物线C交于D,E两点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)<f(b)<f(c) | B. | f(b)<f(c)<f(a) | C. | f(b)<f(a)<f(c) | D. | f(c)<f(a)<f(b) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 劳动生产率为1 000元时,工资为110元 | |
| B. | 劳动生产率提高1 000元,则工资提高60元 | |
| C. | 劳动生产率提高1 000元,则工资提高110元 | |
| D. | 当月工资为210元时,劳动生产率为1 500元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com