Question

4．设m∈R，实数x，y满足$\left\{\begin{array}{l}x≥m\\ 2x-3y+6≥0\\ 3x-2y-6≤0\end{array}\right.$，若|x+2y|≤18，则实数m的取值范围是[-3，6]．

Answer 1

分析 由题意作平面区域，从而可得A（6，6），B（m，$\frac{3m}{2}$-3），从而可得m+2（$\frac{3m}{2}$-3）≥-18，从而求得．

解答 解：由题意作不等式组$\left\{\begin{array}{l}x≥m\\ 2x-3y+6≥0\\ 3x-2y-6≤0\end{array}\right.$表示的平面区域如下，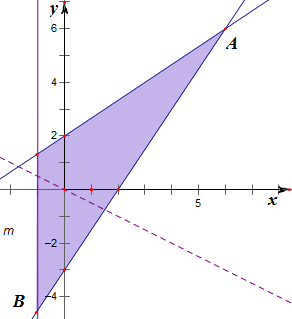
，
结合图象可知，A（6，6），B（m，$\frac{3m}{2}$-3），
易知m≤6，
且m+2（$\frac{3m}{2}$-3）≥-18，
解得m≥-3，
故-3≤m≤6．
故答案为：[-3，6]．

点评 本题考查了线性规划，同时考查了学生的作图能力及数形结合的思想方法的应用，属于中档题．