
| A. | 1 | B. | 2 | C. | 3 | D. | 无数个 |
分析 将求g(x)=f(x)-log2x的零点个数,转化成求f(x)=n-1,x∈[n,n+1],n∈N,与h(x)=log2x交点个数,分别绘制f(x)和h(x)函数图象,根据函数图象及函数解析式即可f(x)和h(x)得交点个数.
解答 解:将求g(x)=f(x)-log2x的零点个数,转化成求f(x)=n-1,x∈[n,n+1],n∈N,与h(x)=log2x交点个数,
画出f(x)和h(x)在同一坐标系中函数图象,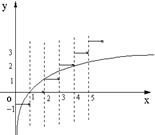
①当n=0时,f(x)=-1,x∈[0,1),则log2x=-1⇒x=$\frac{1}{2}$∈[0,1)成立,
②当n=1时,f(x)=0,x∈[1,2),则log2x=0⇒x=1∈[1,2),
③当n=2时,f(x)=1,x∈[2,3),则log2x=1⇒x=2∈[2,3),
④当n=3时,f(x)=2,x∈[3,4),则log2x=2⇒x=4∉[3,4),
⑤当n=4时,f(x)=3,x∈[4,5),则log2x=3⇒x=8∉[4,5),
∴从第二项起x的取值以1为首项2为公比的等比数列,而区间函数f(x)成正比增长,
故f(x)和h(x)没有交点,
∴f(x)和h(x)由三个交点,
∴函数g(x)=f(x)-log2x有3个零点,
故答案选:C.
点评 本题考查根的存在性与根的个数判断问题,考查数形结合的思想、分类讨论的思想以及问题转化的思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 劳动生产率为1 000元时,工资为110元 | |
| B. | 劳动生产率提高1 000元,则工资提高60元 | |
| C. | 劳动生产率提高1 000元,则工资提高110元 | |
| D. | 当月工资为210元时,劳动生产率为1 500元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.
如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -log20122011 | B. | -1 | C. | -1+log20122011 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 患心脏病 | 患其它病 | 合 计 | |
| 高血压 | 20 | 10 | 30 |
| 不高血压 | 30 | 50 | 80 |
| 合 计 | 50 | 60 | 110 |
| A. | 有99%以上的把握认为“高血压与患心脏病无关” | |
| B. | 有99%以上的把握认为“高血压与患心脏病有关” | |
| C. | 在犯错误的概率不超过0.1%的前提下,认为“高血压与患心脏病无关” | |
| D. | 在犯错误的概率不超过0.1%的前提下,认为“高血压与患心脏病有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
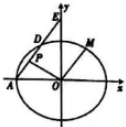 如图,在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2\sqrt{2}}{3}$,经过椭圆的左顶点A(-3,0)作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴与点E.
如图,在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2\sqrt{2}}{3}$,经过椭圆的左顶点A(-3,0)作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴与点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com