
���� ��1��ֱ�����õȲ����еĶ�����4an+1��1-an��=1֤������{bn}Ϊ�Ȳ����У�
��2���ɣ�1���еĵȲ������������{an}��ͨ��ɵ�$\frac{{a}_{n+1}}{{a}_{n}}$��Ȼ����������������ͣ��ɵ�$\frac{{a}_{2}}{{a}_{1}}+\frac{{a}_{3}}{{a}_{2}}+\frac{{a}_{4}}{{a}_{3}}$+��+$\frac{{a}_{n+1}}{{a}_{n}}$��n+1��
��� ֤������1����bn=$\frac{1}{2{a}_{n}-1}$��
��${b}_{n+1}-{b}_{n}=\frac{1}{2{a}_{n+1}-1}-\frac{1}{2{a}_{n}-1}$=$\frac{2{a}_{n}-2{a}_{n+1}}{4{a}_{n+1}{a}_{n}-2{a}_{n}-2{a}_{n+1}+1}$��
��4an+1��1-an��=1��
��${b}_{n+1}-{b}_{n}=\frac{2{a}_{n}-2{a}_{n+1}}{4{a}_{n+1}{a}_{n}-2{a}_{n}-2{a}_{n+1}+4{a}_{n+1}��1-{a}_{n}��}=-1$��
������{bn}Ϊ������-1������Ϊ-2�ĵȲ����У�
��2��������{bn}Ϊ������-1������Ϊ-2�ĵȲ����У�
��$\frac{1}{2{a}_{n}-1}=-1-n$����${a}_{n}=\frac{n}{n+1}$��
��$\frac{{a}_{n+1}}{{a}_{n}}=\frac{n+1}{n+2}•\frac{n+1}{n}=1+\frac{1}{n��n+2��}=1+\frac{1}{2}��\frac{1}{n}-\frac{1}{n+2}��$��
��$\frac{{a}_{2}}{{a}_{1}}+\frac{{a}_{3}}{{a}_{2}}+\frac{{a}_{4}}{{a}_{3}}$+��+$\frac{{a}_{n+1}}{{a}_{n}}$=n+$\frac{1}{2}$[$��1-\frac{1}{3}��+��\frac{1}{2}-\frac{1}{4}��+��\frac{1}{3}-\frac{1}{5}��+��+��\frac{1}{n}-\frac{1}{n+2}��$]
=$n+\frac{1}{2}��1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2}����n+1$��
���� �����������벻��ʽ���ۺ��⣬�����˵Ȳ��ϵ��ȷ����ѵ�������������������еĺͣ����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
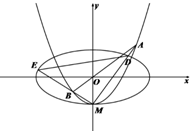 ��ͼ����֪��ԲC1��$\frac{x^2}{4}$+y2=1������C2��y=x2-1��y��Ľ���ΪM��������ԭ��O��ֱ��l��C2�ཻ��A��B���㣬ֱ��MA��MB�ֱ���C1�ཻ��D��E���㣬ֱ��MA��MB��б�ʷֱ�Ϊk1��k2
��ͼ����֪��ԲC1��$\frac{x^2}{4}$+y2=1������C2��y=x2-1��y��Ľ���ΪM��������ԭ��O��ֱ��l��C2�ཻ��A��B���㣬ֱ��MA��MB�ֱ���C1�ཻ��D��E���㣬ֱ��MA��MB��б�ʷֱ�Ϊk1��k2�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [$\frac{��}{3}$��$\frac{5��}{6}$] | B�� | [0��$\frac{��}{3}$] | C�� | [$\frac{��}{6}$��$\frac{��}{2}$] | D�� | [$\frac{��}{6}$��$\frac{5��}{6}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com