
| A. | [$\frac{π}{3}$,$\frac{5π}{6}$] | B. | [0,$\frac{π}{3}$] | C. | [$\frac{π}{6}$,$\frac{π}{2}$] | D. | [$\frac{π}{6}$,$\frac{5π}{6}$] |
分析 计算向量$\overrightarrow{CA}$的模长,得到点A在以C(0,2)为圆心,$\sqrt{3}$为半径的圆上,利用数形结合,由图来分析其夹角的最大值、最小值点,结合解三角形的有关知识进而得到答案.
解答 解:∵$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(0,2),$\overrightarrow{CA}$=($\sqrt{3}$cosα,$\sqrt{3}$sinα),
∴|$\overrightarrow{CA}$|=$\sqrt{3cos^2α+3sin^2α}$=$\sqrt{3}$,
A的轨迹是以C(2,0)为圆心,以$\sqrt{3}$为半径的圆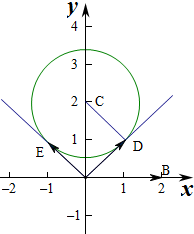
在△COD中,OC=2,CD=$\sqrt{3}$,∠CDO=$\frac{π}{2}$,所以∠COD=$\frac{π}{3}$,
所以当A在D处时,则 $\overrightarrow{OA}$与 $\overrightarrow{OB}$夹角最小为 $\frac{π}{2}-\frac{π}{3}=\frac{π}{6}$,
当A在E处时 $\overrightarrow{OA}$与 $\overrightarrow{OB}$夹角最大为 $\frac{π}{2}+\frac{π}{3}=\frac{5π}{6}$,
∴$\overrightarrow{OA}$与 $\overrightarrow{OB}$夹角的取值范围是[$\frac{π}{6},\frac{5π}{6}$],
故选:D.
点评 本题考查向量的坐标运算及向量的数量积与夹角的计算,根据条件利用向量模长的几何意义,转化为数形结合是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-∞,-$\frac{1}{2}$)∪(2,+∞) | C. | (-$\frac{1}{2}$,2) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{2}{11}$ | C. | 2 | D. | $\frac{5}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
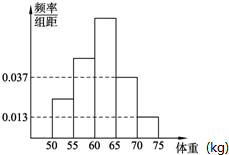 某省组织部为了了解今年全省高三毕业班准备报考飞行员的学生的体重情况,对该省某校高三毕业班准备报考飞行员的学生的体重进行了统计,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
某省组织部为了了解今年全省高三毕业班准备报考飞行员的学生的体重情况,对该省某校高三毕业班准备报考飞行员的学生的体重进行了统计,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com