
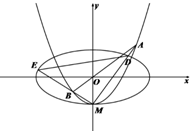
 如图,已知椭圆C1:$\frac{x^2}{4}$+y2=1,曲线C2:y=x2-1与y轴的交点为M,过坐标原点O的直线l与C2相交于A,B两点,直线MA,MB分别与C1相交于D,E两点,直线MA,MB的斜率分别为k1,k2
如图,已知椭圆C1:$\frac{x^2}{4}$+y2=1,曲线C2:y=x2-1与y轴的交点为M,过坐标原点O的直线l与C2相交于A,B两点,直线MA,MB分别与C1相交于D,E两点,直线MA,MB的斜率分别为k1,k2分析 (1)设过原点的直线l:y=tx,联立$\left\{\begin{array}{l}{y=tx}\\{y={x}^{2}-1}\end{array}\right.$,得x2-ty-1=0,从而求出$\overrightarrow{MA}•\overrightarrow{MB}$=0,由此能求出k1k2.
(2)设直线MA:y=k1x-1,直线MB:y=-$\frac{1}{{k}_{1}}$x-1,联立$\left\{\begin{array}{l}{y={k}_{1}x-1}\\{y={x}^{2}-1}\end{array}\right.$,得A(${k}_{1},{{k}_{1}}^{2}-1$),联立$\left\{\begin{array}{l}{y={k}_{1}x-1}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得D($\frac{8{k}_{1}}{4{{k}_{1}}^{2}+1}$,$\frac{4{{k}_{1}}^{2}-1}{4{{k}_{1}}^{2}+1}$),同理,得B(-$\frac{1}{{k}_{1}}$,$\frac{1}{{{k}_{1}}^{2}}$-1),E($\frac{-8{k}_{1}}{4+{{k}_{1}}^{2}}$,$\frac{4-{{k}_{1}}^{2}}{4+{{k}_{1}}^{2}}$),由此能求出λ的取值范围.
解答 解:(1)设A(x1,y1),B(x2,y2),E(x3,y3),E(x4,y4),过原点的直线l:y=tx,
联立$\left\{\begin{array}{l}{y=tx}\\{y={x}^{2}-1}\end{array}\right.$,得x2-ty-1=0,
$\overrightarrow{MA}$=(x1,y1+1),$\overrightarrow{MB}$=(x2,y2+1),
$\overrightarrow{MA}•\overrightarrow{MB}$=x1x2+(y1+1)(y2+1)=(t2+1)x1x2+t(x1+x2)+1=0,
∴$\overrightarrow{MA}$⊥$\overrightarrow{MB}$,
∴k1k2=-1.
(2)设直线MA:y=k1x-1,直线MB:y=-$\frac{1}{{k}_{1}}$x-1,
联立$\left\{\begin{array}{l}{y={k}_{1}x-1}\\{y={x}^{2}-1}\end{array}\right.$,得A(${k}_{1},{{k}_{1}}^{2}-1$),
联立$\left\{\begin{array}{l}{y={k}_{1}x-1}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得D($\frac{8{k}_{1}}{4{{k}_{1}}^{2}+1}$,$\frac{4{{k}_{1}}^{2}-1}{4{{k}_{1}}^{2}+1}$),
同理,得B(-$\frac{1}{{k}_{1}}$,$\frac{1}{{{k}_{1}}^{2}}$-1),E($\frac{-8{k}_{1}}{4+{{k}_{1}}^{2}}$,$\frac{4-{{k}_{1}}^{2}}{4+{{k}_{1}}^{2}}$),
$\overrightarrow{MA}$=(${k}_{1},{k}_{1}{\;}^{2}$),$\overrightarrow{MB}$=(-$\frac{1}{{k}_{1}}$,$\frac{1}{{{k}_{1}}^{2}}$),$\overrightarrow{MD}$=($\frac{8{k}_{1}}{4{{k}_{1}}^{2}+1}$,$\frac{8{{k}_{1}}^{2}}{4{{k}_{1}}^{2}+1}$),$\overrightarrow{ME}$=($\frac{-8{k}_{1}}{4+{{k}_{1}}^{2}}$,$\frac{8}{4+{{k}_{1}}^{2}}$),
∴S1=$\frac{1}{2}$|${k}_{1}+\frac{1}{{k}_{1}}$|,S2=$\frac{1}{2}$|$\frac{8{k}_{1}}{4{{k}_{1}}^{2}+1}$×$\frac{8}{4+{{k}_{1}}^{2}}$+$\frac{8{{k}_{1}}^{2}}{4{{k}_{1}}^{2}+1}$×$\frac{8{k}_{1}}{4{{+k}_{1}}^{2}}$|=$\frac{32|{k}_{1}|({{k}_{1}}^{2}+1)}{(4{{k}_{1}}^{2}+1)(4+{{k}_{1}}^{2})}$,
∴λ=$\frac{(4{{k}_{1}}^{2}+1)({{k}_{1}}^{2}+4)}{64{{k}_{1}}^{2}}$=$\frac{1}{64}$(4k12+$\frac{4}{{{k}_{1}}^{2}}$+17)≥$\frac{25}{64}$.
当且仅当$4{{k}_{1}}^{2}=\frac{4}{{{k}_{1}}^{2}}$,即k1=±1时,取等号,
∴λ的取值范围[$\frac{25}{64}$,+∞).
点评 本题考查两直线的斜率乘积的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | (-∞,-2) | C. | (-2,+∞) | D. | (-∞,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-∞,-$\frac{1}{2}$)∪(2,+∞) | C. | (-$\frac{1}{2}$,2) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com