
| A. | (-∞,-2] | B. | (-∞,-2) | C. | (-2,+∞) | D. | (-∞,2) |
分析 由原函数有两个极值,可知其导函数有两个不同的实数根,转化为直线y=-ax-a与曲线y=2ex有两个不同交点求解.
解答 解:由f(x)=2ex+$\frac{1}{2}$ax2+ax+1,
得f′(x)=2ex+ax+a,
要使f(x)=2ex+$\frac{1}{2}$ax2+ax+1有两个极值,
则方程2ex+ax+a=0有两个不同的实数根,
即2ex=-ax-a有两个不同的实数根,
令y=2ex,y=-ax-a,
直线y=-a(x+1)过点(-1,0),设直线y=-a(x+1)与y=2ex的切点为(x0,$2{e}^{{x}_{0}}$).
则y′=$2{e}^{{x}_{0}}$,
则切线方程为y-$2{e}^{{x}_{0}}$=$2{e}^{{x}_{0}}$(x-x0),
代入(-1,0),得-$2{e}^{{x}_{0}}$=$2{e}^{{x}_{0}}$(-1-x0),解得:x0=0.
∴切点为(0,2),则过(-1,0),(0,2)切线的斜率为k=$\frac{2-0}{0-(-1)}$=2,
由-a>2,得a<-2.
∴实数a的取值范围为a<-2.
故选:B.
点评 本题考查利用导数求函数的极值,考查了数学转化思想方法,求出过(-1,0)与曲线相切的直线的斜率是关键,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2-1 | B. | f(x)=2x+1 | ||
| C. | f(x)=$\left\{\begin{array}{l}{{x}^{2}+1(x>1)}\\{{x}^{2}-1(x≤1)}\end{array}\right.$ | D. | f(x)=2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$=$\overrightarrow{b}$ | B. | $\overrightarrow{a}$∥$\overrightarrow{b}$,且$\overrightarrow{a}$,$\overrightarrow{b}$方向相同 | ||
| C. | $\overrightarrow{a}$=-$\overrightarrow{b}$ | D. | $\overrightarrow{a}$∥$\overrightarrow{b}$,且$\overrightarrow{a}$,$\overrightarrow{b}$方向相反 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 商店名称 | A | B | C | D | E |
| 销售额x (千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y (百万元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在?ABCD中,点E为边AB的中点,BD与CE交于点P,若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$(x,y∈R),则2x+y=$\frac{5}{3}$;若点Q是△BCP内部(包括边界)一动点,且$\overrightarrow{AQ}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n∈R),则m+2n的取值范围为[1,3].
如图,在?ABCD中,点E为边AB的中点,BD与CE交于点P,若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$(x,y∈R),则2x+y=$\frac{5}{3}$;若点Q是△BCP内部(包括边界)一动点,且$\overrightarrow{AQ}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n∈R),则m+2n的取值范围为[1,3].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{2}}$] | B. | (-∞,-1] | C. | [${\frac{1}{2}$,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
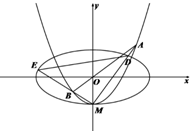 如图,已知椭圆C1:$\frac{x^2}{4}$+y2=1,曲线C2:y=x2-1与y轴的交点为M,过坐标原点O的直线l与C2相交于A,B两点,直线MA,MB分别与C1相交于D,E两点,直线MA,MB的斜率分别为k1,k2
如图,已知椭圆C1:$\frac{x^2}{4}$+y2=1,曲线C2:y=x2-1与y轴的交点为M,过坐标原点O的直线l与C2相交于A,B两点,直线MA,MB分别与C1相交于D,E两点,直线MA,MB的斜率分别为k1,k2查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com