Question

【题目】已知命题函数在上是减函数，命题 ，．

（1）若为假命题，求实数的取值范围；

（2）若“或”为假命题，求实数的取值范围．

Answer 1

【答案】（1）；（2）

【解析】分析：第一问利用命题的否定和命题本身是一真一假的，根据命题q是假命题，得到命题的否定是真命题，结合二次函数图像，得到相应的参数的取值范围；第二问利用“或”为假命题，则有两个命题都是假命题，所以先求命题p为真命题时参数的范围，之后求其补集，得到m的范围，之后将两个命题都假时参数的范围取交集，求得结果.

详解：（1）因为命题 ，

所以： ，，

当为假命题时，等价于为真命题，

即在上恒成立，

故，解得

所以为假命题时，实数的取值范围为.

（2）函数的对称轴方程为，

当函数在上是减函数时，则有

即为真时，实数的取值范围为

“或”为假命题，故与同时为假，

则 ，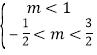

综上可知，当 “或”为假命题时，实数的取值范围为