
给出下列四个结论:① 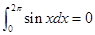 ;
;
②已知集合 ,若
,若 ,则
,则 1
1
③已知 为定义在R上的可导函数,且
为定义在R上的可导函数,且 对于
对于 恒成立,则有
恒成立,则有 ,
,  ;
;
④ 若定义在正整数有序对集合上的二元函数 满足:(1)
满足:(1) ,(2)
,(2) (3)
(3) ,则
,则 =
=
则其中正确结论的有 (填写你认为正确的序号)
①③④
【解析】
试题分析:对于① 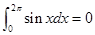 ,正确;对于② 已知集合
,正确;对于② 已知集合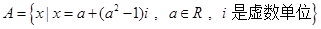 ,若
,若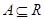 ,则
,则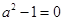 ,所以
,所以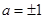 ,错误;对于③ 设
,错误;对于③ 设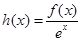 ,∵
,∵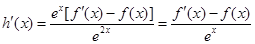 ,且
,且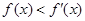 ,∴
,∴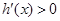 ,∴函数h(x)在定义域上单调递增,则有
,∴函数h(x)在定义域上单调递增,则有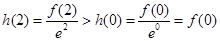 即
即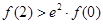 ,
,  即
即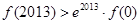 ,正确;对于④由
,正确;对于④由 可得 f(x,x+y)=(x+y)f(x,y)/y,又因为f(x,y)=f(y,x),f(x,x)=x,∴f(12,16)=f(12,12+4)="(12+4)f(12,4)/4=4f(12,4)=4f(4,12)=4f(4,4+8)"
="4(4+8)f(4,8)/8=6f(4,8)"
="6f(4,4+4)=6(4+4)f(4,4)/4=12f(4,4)" =12×4=48,所以
可得 f(x,x+y)=(x+y)f(x,y)/y,又因为f(x,y)=f(y,x),f(x,x)=x,∴f(12,16)=f(12,12+4)="(12+4)f(12,4)/4=4f(12,4)=4f(4,12)=4f(4,4+8)"
="4(4+8)f(4,8)/8=6f(4,8)"
="6f(4,4+4)=6(4+4)f(4,4)/4=12f(4,4)" =12×4=48,所以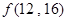 =
=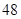 ,正确,综上正确的结论有①③④
,正确,综上正确的结论有①③④
考点:本题考查了导数的运用、定积分的求解等
点评:此类问题比较综合,考查了学生的逻辑分析能力和解决问题的能力


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2x-1 |
| 1 |
| 3x-1 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,正方体ABCD-A1B1C1D1的棱长为1,线段AC1上有两个动点E,F,且EF=
如图,正方体ABCD-A1B1C1D1的棱长为1,线段AC1上有两个动点E,F,且EF=
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a | b |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com