
分析 由题意可得弦所在直线的斜率存在,设为k,可得直线方程为y=kx+m,(k≠0),代入抛物线的方程,运用韦达定理和判别式大于0,弦长公式,运用换元法,以及函数的单调性和抛物线的对称性,即可得到所求范围.
解答 解:由题意可得弦所在直线的斜率存在,设为k,
可得直线方程为y=kx+m,(k≠0),
代入抛物线的方程,可得x2-kx-m=0,
即有△=k2+4m>0,
设弦的端点的横坐标分别为x1,x2,
可得x1+x2=k,x1x2=-m,
即有弦长为$\sqrt{1+{k}^{2}}$|x1-x2|=$\sqrt{1+{k}^{2}}$•$\sqrt{{k}^{2}+4m}$=2,
化为4m=$\frac{4}{1+{k}^{2}}$-k2,
令t=1+k2(t>1),即有f(t)=$\frac{4}{t}$-t+1递减,
则f(t)<4,即有4m<4,解得m<1.
检验由抛物线关于y轴对称,成立.
故答案为:(-∞,1).
点评 本题考查抛物线的方程和运用,注意联立直线方程,运用韦达定理和判别式大于0,以及弦长公式,考查运算能力和转化思想,属于中档题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
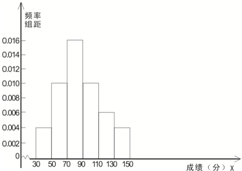 某省去年高三100000名考生英语成绩服从正态公布N(85,225),现随机抽取50名考生的成绩,发现全部介于[30,150]之间,将成绩按如下方式分成6组:第一组[30,50),第二组[50,70),…第6组[130,150],如图是按上述分组方法得到的频率分布直方图.
某省去年高三100000名考生英语成绩服从正态公布N(85,225),现随机抽取50名考生的成绩,发现全部介于[30,150]之间,将成绩按如下方式分成6组:第一组[30,50),第二组[50,70),…第6组[130,150],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{13}$ | B. | 10 | C. | 2$\sqrt{37}$ | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}+2\sqrt{2}}{6}$ | B. | $\frac{\sqrt{3}-2\sqrt{2}}{6}$ | C. | $\frac{1+2\sqrt{6}}{6}$ | D. | $\frac{1-2\sqrt{6}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com