
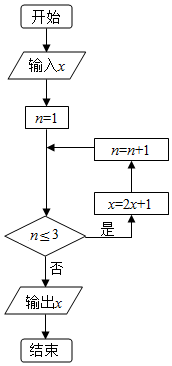
 执行如图所示的程序框图,若输出值x∈(16,25),则输入x的值可以是( )
执行如图所示的程序框图,若输出值x∈(16,25),则输入x的值可以是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 模拟执行程序框图,依次写出每次循环得到的x,n的值,当n=4时,不满足条件n≤3,退出循环,输出x的值,由x=2[2(2x+1)+1]+1=8x+7∈(16,25),结合各个选项即可得解.
解答 解:模拟执行程序框图,可得
n=1
满足条件n≤3,执行循环体,x=2x+1,n=2
满足条件n≤3,执行循环体,x=2(2x+1)+1,n=3
满足条件n≤3,执行循环体,x=2[2(2x+1)+1]+1,n=4
不满足条件n≤3,退出循环,输出x的值.
∵由题意可得:x=2[2(2x+1)+1]+1=8x+7∈(16,25),
∴可解得:$\frac{9}{8}$<x<$\frac{9}{4}$,对比各个选项,则输入x的值可以是2.
故选:B.
点评 本题主要考查了程序框图和算法的应用,模拟执行程序框图,得到退出循环时x=2[2(2x+1)+1]+1=8x+7是解题的关键,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
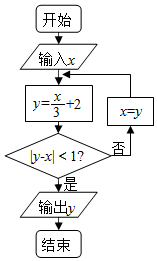
| A. | $\frac{4}{3}$ | B. | $\frac{11}{3}$ | C. | $\frac{29}{9}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,一平面与空间四边形ABCD的对角线AC,BD都平行,且交空间四边形的边AB,BC,CD,DA分别于E,F,G,H.
如图,一平面与空间四边形ABCD的对角线AC,BD都平行,且交空间四边形的边AB,BC,CD,DA分别于E,F,G,H.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若f(2)≤4成立,则当k≥1时,均有f(k)≤k2成立 | |
| B. | 若f(4)≤16成立,则当k≤4时,均有f(k)≤k2成立 | |
| C. | 若f(6)>36成立,则当k≥7时,均有f(k)>k2成立 | |
| D. | 若f(7)=50成立,则当k≤7时,均有f(k)>k2成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 每组员工编号 | 1 | 2 | 3 | 4 | 5 |
| 甲组 | a | 5 | 7 | 9 | b |
| 乙组 | 5 | 6 | 7 | 8 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com