
| 每组员工编号 | 1 | 2 | 3 | 4 | 5 |
| 甲组 | a | 5 | 7 | 9 | b |
| 乙组 | 5 | 6 | 7 | 8 | 9 |
分析 (1)由表中数据我们易求出两组数据的平均数,代入方差公式后,即可求出a,b的值,再比较哪一组技工的技术水平的稳定性更好.
(2)要计算该车间“质量合格”的概率,我们要先求出从甲、乙两组中各抽取1名技工完成合格零件个数的基本事件总个数,再求出该车间“质量合格”包含的基本事件个数,代入古典概型概率公式,即可求出答案.
解答 解:(1)由甲组技工在单位时间内完成合格零件的平均数与方差分别为7与5.2,得$\left\{\begin{array}{l}\frac{a+5+7+9+b}{5}=7\\ \frac{{{{(a-7)}^2}+{{(5-7)}^2}+{{(7-7)}^2}+{{(9-7)}^2}+{{(b-7)}^2}}}{5}=5.2\end{array}\right.$…(2分)
即$\left\{\begin{array}{l}a+b=14\\{(a-7)^2}+{(b-7)^2}=18\end{array}\right.$,解得$\left\{\begin{array}{l}a=4\\ b=10\end{array}\right.或\left\{\begin{array}{l}a=10\\ b=4\end{array}\right.$
又a<b,
故a的值为4,b的值为10,…(5分)
且乙组技工的技术水平的稳定性更好.…(7分)
(2)设事件 A表示:该车间“质量合格”,则从甲、乙两组中各抽取1名技工完成合格零件个数的基本事件为(4,5),(4,6),(4,7),(4,8),(4,9),(5,5),(5,6),(5,7),(5,8),(5,9),(7,5),(7,6),(7,7),(7,8),(7,9),(9,5),(9,6),(9,7),(9,8),(9,9),(10,5),(10,6),(10,7),(10,8),(10,9)共25种.…(9分)
事件 A包含的基本事件为(4,9),(5,8),(5,9),(7,6),(7,7),(7,8),(7,9),(9,5),(9,6),(9,7),(9,8),(9,9),(10,5),(10,6),(10,7),(10,8),(10,9)共17种.…(10分)
∴${P}({A})=\frac{17}{25}$.即该车间“质量合格”的概率为$\frac{17}{25}$.…(12分)
点评 本题主要考查在实际背景下,将统计与概率相结合,考查了样本的平均数与方差的计算,以及求随机事件的概率,考查了归纳推理、应用数学知识解决实际问题的能力.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中数学 来源: 题型:解答题
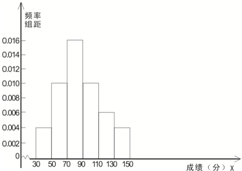 某省去年高三100000名考生英语成绩服从正态公布N(85,225),现随机抽取50名考生的成绩,发现全部介于[30,150]之间,将成绩按如下方式分成6组:第一组[30,50),第二组[50,70),…第6组[130,150],如图是按上述分组方法得到的频率分布直方图.
某省去年高三100000名考生英语成绩服从正态公布N(85,225),现随机抽取50名考生的成绩,发现全部介于[30,150]之间,将成绩按如下方式分成6组:第一组[30,50),第二组[50,70),…第6组[130,150],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-$\frac{1}{π}$ | B. | 1-$\frac{2}{π}$ | C. | 1-$\frac{3}{π}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com