
分析 (Ⅰ)先证明an+1-an>0,再证明an+1<1.
(Ⅱ)由ak+12+ak+1-1=ak2,对k取1,2,…,n-1时的式子相加得Sn,最后对Sn进行放缩即可证得.
(Ⅲ)利用放缩法由${a_{k+1}}^2+{a_{k+1}}=1+{a_k}^2≥2{a_k}$,得$\frac{1}{{1+{a_{k+1}}}}≤\frac{{{a_{k+1}}}}{{2{a_k}}}(k=2,3,…,n-1,n≥3)$,即可得出结论.
解答 证明:(Ⅰ)因为an+12+an+1-1=an2,(1)所以an2+an-1=an-12,(2)
$(1)-(2)得({a_{n+1}}-{a_n})({a_{n+1}}+{a_n}+1)=a_n^2-a_{n-1}^2$,
所以an+1-an与an-an-1同号,即与a2-a1一致.
因为${a_2}=\frac{{-1+\sqrt{5}}}{2}$,且a2-a1>0,
∴an+1-an>0,
∵$a_{n+1}^2+{a_{n+1}}-1=a_n^2$,
∴$a_{n+1}^2-a_n^2=1-{a_{n+1}}>0$,
即an+1<1
综上所述:0≤an<an+1<1对任何n∈N*都成立.
(Ⅱ)证明:由${a_{k+1}}^2+{a_{k+1}}-1={a_k}^2$,k=1,2,…,n-1(n≥2),
得$a_n^2+({a_2}+{a_3}+…+{a_n})-(n-1)=a_1^2$.
因为a1=0,所以${S_n}=n-1-a_n^2$.
∵an<1,
所以Sn>n-2.
(Ⅲ)证明:由${a_{k+1}}^2+{a_{k+1}}=1+{a_k}^2≥2{a_k}$,得$\frac{1}{{1+{a_{k+1}}}}≤\frac{{{a_{k+1}}}}{{2{a_k}}}(k=2,3,…,n-1,n≥3)$
所以$\frac{1}{{(1+{a_3})(1+{a_4})…(1+{a_n})}}≤\frac{a_n}{{{2^{n-2}}{a_2}}}(a≥3)$,
于是$\frac{1}{{(1+{a_2})(1+{a_3})…(1+{a_n})}}≤\frac{a_n}{{{2^{n-2}}(a_2^2+{a_2})}}=\frac{a_n}{{{2^{n-2}}}}<\frac{1}{{{2^{n-2}}}}(n≥3)$,
故当n≥3时,${T_n}<1+1+\frac{1}{2}+…+\frac{1}{{{2^{n-2}}}}<3$,
又因为T1<T2<T3,
所以Tn<3.
点评 本题主要考查数列的递推关系,不等式证明等基础知识和基本技能,同时考查逻辑推理能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,一平面与空间四边形ABCD的对角线AC,BD都平行,且交空间四边形的边AB,BC,CD,DA分别于E,F,G,H.
如图,一平面与空间四边形ABCD的对角线AC,BD都平行,且交空间四边形的边AB,BC,CD,DA分别于E,F,G,H.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-2,1] | C. | (1,2) | D. | [1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 每组员工编号 | 1 | 2 | 3 | 4 | 5 |
| 甲组 | a | 5 | 7 | 9 | b |
| 乙组 | 5 | 6 | 7 | 8 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
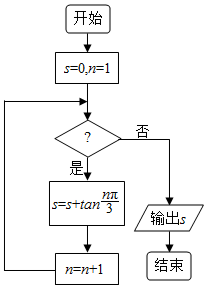 阅读如图所示的程序框图,若运行相应的程序输出的结果为0,则判断框中的条件不可能是( )
阅读如图所示的程序框图,若运行相应的程序输出的结果为0,则判断框中的条件不可能是( )| A. | n≤2014 | B. | n≤2015 | C. | n≤2016 | D. | n≤2018 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{18}$ | B. | -$\frac{17}{18}$ | C. | $\frac{18}{17}$ | D. | -$\frac{18}{17}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com