
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
科目:高中数学 来源: 题型:解答题
| 每组员工编号 | 1 | 2 | 3 | 4 | 5 |
| 甲组 | a | 5 | 7 | 9 | b |
| 乙组 | 5 | 6 | 7 | 8 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$或$\frac{1}{5}$ | D. | $\frac{1}{3}$或$\frac{1}{5}$或0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{18}$ | B. | -$\frac{17}{18}$ | C. | $\frac{18}{17}$ | D. | -$\frac{18}{17}$ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(理)试卷(解析版) 题型:解答题
已知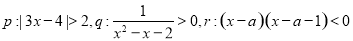 .
.
(1)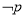 是
是 的什么条件?
的什么条件?
(2)若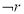 是
是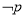 的必要非充分条件,求实数
的必要非充分条件,求实数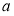 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:解答题
已知函数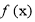 的定义域为
的定义域为 ,对于任意的
,对于任意的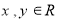 ,都有
,都有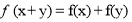 ,且当
,且当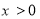 时,
时, ,若
,若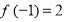 .
.
(1) 求证: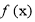 是
是 上的减函数;
上的减函数;
(2) 求函数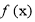 在区间
在区间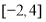 上的值域.
上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com