
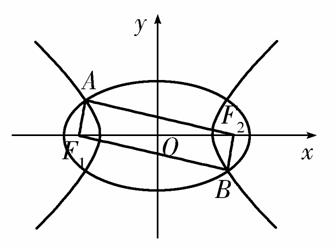
如图,F1、F2是椭圆C1: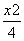 +y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )
+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )
A.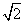 B.
B.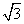
C.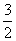 D.
D.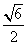
D
[解析] 不妨设双曲线方程为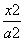 -
-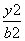 =1.
=1.
由题意知|BF1|-|BF2|=2a⇒|BF1|2+|BF2|2-2|BF1|·|BF2|=4a2,①
并由勾股定理得|BF1|2+|BF2|2=4c2=12,②
由①②知12-4a2=2|BF1|·|BF2|,
∴|BF1|·|BF2|=6-2a2.下面求|BF1|·|BF2|的值.
在椭圆中|BF1|+|BF2|=4,故|BF1|2+|BF2|2+2|BF1|·|BF2|=16,
又由②知|BF1|2+|BF2|2=4c2=12,
∴|BF1|·|BF2|=2,因此有c2-a2=1,
∵c2=3,∴a2=2,∴C2的离心率e=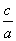 =
=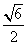 .
.


科目:高中数学 来源: 题型:
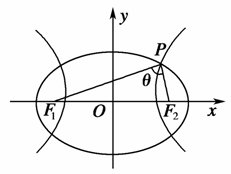
已知椭圆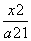 +
+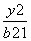 =1(a1>b1>0)与双曲线
=1(a1>b1>0)与双曲线 -
-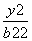 =1(a2>0,b2>0)有公共焦点F1、F2,设P是它们的一个交点.
=1(a2>0,b2>0)有公共焦点F1、F2,设P是它们的一个交点.
(1)试用b1,b2表示△F1PF2的面积;
(2)当b1+b2=m(m>0)是常数时,求△F1PF2的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
设f0(x)=sinx,f1(x)=f ′0(x),f2(x)=f ′1(x),…,fn+1(x)=f ′n(x),n∈N,则f2 015(x)等于( )
A.sinx B.-sinx
C.cosx D.-cosx
查看答案和解析>>
科目:高中数学 来源: 题型:
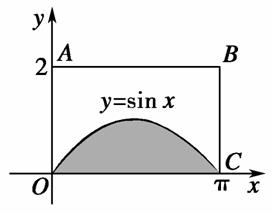
如图所示,在一个长为π,宽为2的矩形OABC内,曲线y=sinx(0≤x≤π)与x轴围成如图所示的阴影部分,向矩形OABC内随机投一点(该点落在矩形OABC内任何一点是等可能的),则所投的点落在阴影部分的概率是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com