
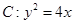 ,过点
,过点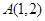 作抛物线
作抛物线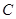 的弦
的弦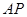 ,
,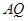 .
.
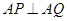 ,证明直线
,证明直线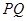 过定点,并求出定点的坐标;
过定点,并求出定点的坐标;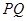 过点
过点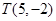 ,请问是否存在以
,请问是否存在以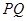 为底边的等腰三角形
为底边的等腰三角形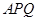 ? 若存在,求出
? 若存在,求出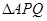 的个数?如果不存在,请说明理由.
的个数?如果不存在,请说明理由.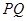 过定点
过定点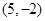 .;(Ⅱ)满足条件的等腰三角形有且只有一个.
.;(Ⅱ)满足条件的等腰三角形有且只有一个.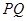 的方程,注意讨论斜率是否存在,与抛物线
的方程,注意讨论斜率是否存在,与抛物线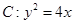 联立,利用
联立,利用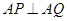 ,转化为坐标运算,数量积为0,找到直线中两个参数的关系,即找到直线过定点;(2)在(1)的条件下,
,转化为坐标运算,数量积为0,找到直线中两个参数的关系,即找到直线过定点;(2)在(1)的条件下,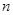 用
用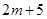 代换,求出
代换,求出 中点
中点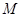 的坐标,用
的坐标,用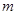 表示,若存在以
表示,若存在以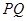 为底边的等腰三角形
为底边的等腰三角形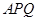 ,也就是
,也就是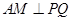 ,整理得关于
,整理得关于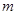 的方程,解方程就得到满足条件的三角形及其个数.
的方程,解方程就得到满足条件的三角形及其个数.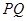 的方程为
的方程为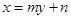 ,点
,点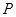 、
、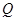 的坐标分别为
的坐标分别为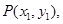
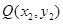 .
. 消
消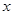 ,得
,得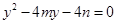 .
.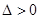 ,得
,得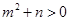 ,
,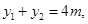
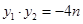 .
.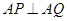 ,∴
,∴ ,∴
,∴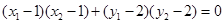 .
.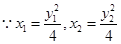
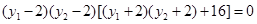 ,
,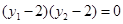 或
或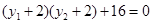 .
.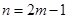 或
或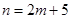 ,∵
,∵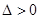 恒成立. ∴
恒成立. ∴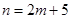 .
.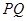 的方程为
的方程为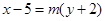 ,∴直线
,∴直线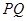 过定点
过定点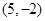 . ………………………………(6分)
. ………………………………(6分)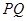 为底边的等腰三角形
为底边的等腰三角形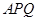 ,由第(Ⅰ)问可知,将
,由第(Ⅰ)问可知,将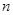 用
用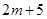 代换得
代换得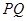 的方程为
的方程为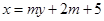 .设点
.设点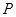 、
、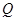 的坐标分别为
的坐标分别为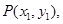
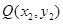 .
.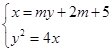 消
消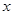 ,得
,得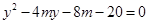 .
.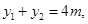
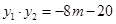 .
.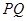 的中点坐标为
的中点坐标为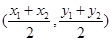 ,即
,即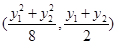 ,
,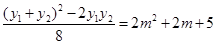 ,∴
,∴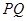 的中点坐标为
的中点坐标为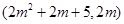 .
.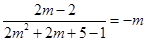 ,即
,即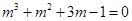 .
. 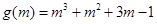 ,则
,则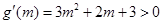 ,
, 在
在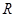 上是增函数.
上是增函数.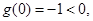
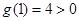 ,
, 在
在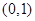 内有一个零点.
内有一个零点.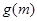 在
在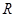 上有且只有一个零点,即方程
上有且只有一个零点,即方程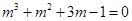 在
在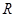 上有唯一实根.
上有唯一实根.

科目:高中数学 来源:不详 题型:填空题
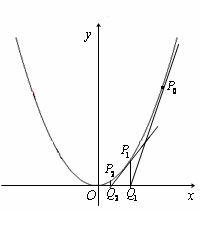
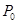 是抛物线
是抛物线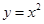 上一点,且在第一象限. 过点
上一点,且在第一象限. 过点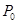 作抛物线的切线,交
作抛物线的切线,交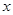 轴于
轴于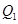 点,过
点,过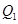 点作
点作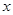 轴的垂线,交抛物线于
轴的垂线,交抛物线于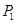 点,此时就称
点,此时就称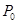 确定了
确定了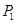 .依此类推,可由
.依此类推,可由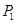 确定
确定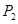 ,
, .记
.记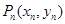 ,
,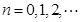 。
。
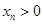 ;
;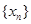 为单调递减数列;
为单调递减数列;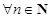 ,
,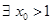 ,使得
,使得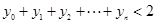 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com