
 给出下列五个命题:
给出下列五个命题:分析 在①中,由系统抽样的原理知样本另一位同学的编号为20;在②中,求出数据的平均数、中位数、众数能判断对错;在③中,求出样本的平均值、样本的方差、标准差,能判断对错;
解答 解:在①中,由系统抽样的原理知抽样的间隔为52÷4=13,
故抽取的样本的编号分别为7,7+13,7+13×2,7+13×3,
即7号、20号、33号、46号,故①是假命题;
在②中,数据1,2,3,3,4,5的平均数为:$\frac{1}{6}$(1+2+3+4+5)=3,
中位数为3,众数为3,都相同,故②是真命题;
在③中,由题可知样本的平均值为1,所以a+0+1+2+3=5,解得a=-1,
故样本的方差为:$\frac{1}{5}$[(-1-1)2+(0-1)2+(1-1)2+(2-1)2+(3-1)2]=2,标准差为$\sqrt{2}$,
故③是假命题;
在④中,一组样本数据中,中位数唯一,众数不一定唯一,
故④是真命题;
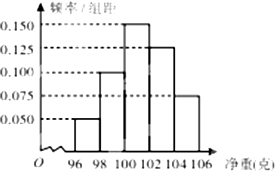
在⑤中,设净重大于或等于98克并且小于104克的产品的个数设为N2,
产品净重小于100克的个数设为N1=36,样本容量为N,
则 $\frac{{N}_{2}}{{N}_{1}}$=$\frac{(0.1+0.5+0.125)×2×N}{(0.05+0.1)×2×N}$=$\frac{375}{150}$,
N2=$\frac{375}{150}$×36=90,
故⑤是真命题,
故答案为:②④⑤.
点评 本考查命题的真假判断,是基础题,解题时要认真审题,注意系统抽样、频率分布直方图、众数、中位数、平均数等知识点的合理运用.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{14}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com