
【题目】某早餐店每天制作甲、乙两种口味的糕点共n(nN*)份,每份糕点的成本1元,售价2元,如果当天卖不完,剩下的糕点作废品处理.该早餐店发现这两种糕点每天都有剩余,为此整理了过往100天这两种糕点的日销量(单位:份),得到如下的统计数据:
甲口味糕点日销量 | 48 | 49 | 50 | 51 |
天数 | 20 | 40 | 20 | 20 |
乙口味糕点日销量 | 48 | 49 | 50 | 51 |
天数 | 40 | 30 | 20 | 10 |
以这100天记录的各销量的频率作为各销量的概率,假设这两种糕点的日销量相互独立.
(1)记该店这两种糕点每日的总销量为X份,求X的分布列
(2)早餐店为了减少浪费,提升利润,决定调整每天制作糕点的份数
①若产生浪费的概率不超过0.6,求n的最大值;
②以销售这两种糕点的日总利润的期望值为决策依据,在每天所制糕点能全部卖完与n=98之中选其一,应选哪个?
【答案】(1)见解析;(2)![]() ,98.
,98.
【解析】试题分析:(1)由题意知![]() 的可能取值为
的可能取值为![]() 分别求出相应的概率,由此能求出
分别求出相应的概率,由此能求出![]() 分布列;(2)①求出
分布列;(2)①求出![]() ,由此能求出n的最大值; ②由(1)知在每天所制蛋糕能全部卖完时,
,由此能求出n的最大值; ②由(1)知在每天所制蛋糕能全部卖完时, ![]() ,此时销售这两种糕点的日总利润的期望值为
,此时销售这两种糕点的日总利润的期望值为![]() ,再求出当
,再求出当![]() 时,销售这两种糕点的日总利润的期望值,由此得到应选
时,销售这两种糕点的日总利润的期望值,由此得到应选![]() .
.
试题解析:(1)X所有可能的取值为96,97,98,99,100,101,102
P(X=96)=0.20.4=0.08
P(X=97)=0.20.3+0.40.4=0.22
P(X=98)= 0.20.2+0.40.3+0.20.4=0.24
P(X=99)= 0.20.1+0.40.2+0.20.3+0.20.4=0.24
P(X=100)= 0.40.1+0.20.2+0.20.3=0.14
P(X=101)= 0.20.1+0.20.2=0.06
P(X=102)= 0.20.1=0.02
X的分布列
X | 96 | 97 | 98 | 99 | 100 | 101 | 102 |
P | 0.08 | 0.22 | 0.24 | 0.24 | 0.14 | 0.06 | 0.02 |
(2)①依题意得,P(X<n)0.6,由P(X<99)=0.54,P(X<100)=0.78,n99
②记销售两种糕点的日总利润为Y,
当每天所制作糕点能全部卖完时,E(Y)96
当n=98时,E(Y)=(96-2)0.08+(97-1)0.22+980.7=97.24>96
选n=98


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 对任意的正整数n,都有an=5Sn+1成立,记bn= ![]() (n∈N*).
(n∈N*).
(1)求数列{an}和数列{bn}的通项公式;
(2)设数列{bn}的前n项和为Rn , 求证:对任意的n∈N* , 都有Rn<4n;
(3)记cn=b2n﹣b2n﹣1(n∈N*),设数列{cn}的前n项和为Tn , 求证:对任意n∈N* , 都有Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C为△ABC的三个内角,且其对边分别为a、b、c,若cosBcosC﹣sinBsinC= ![]() .
.
(1)求角A;
(2)若a=2 ![]() ,b+c=4,求△ABC的面积.
,b+c=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
, ![]() ),
),![]() (
(![]() ),且
),且![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() ,
, ![]() 的值;
的值;
(Ⅱ)若函数![]() 在区间
在区间![]() 内有且仅有一个极值点,求
内有且仅有一个极值点,求![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() (
(![]() )为两曲线
)为两曲线![]() (
(![]() ),
),![]() 的交点,且两曲线在交点
的交点,且两曲线在交点![]() 处的切线分别为
处的切线分别为![]() ,
, ![]() .若取
.若取![]() ,试判断当直线
,试判断当直线![]() ,
, ![]() 与
与![]() 轴围成等腰三角形时
轴围成等腰三角形时![]() 值的个数并说明理由.
值的个数并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=Asin(ωx+φ)(x>0,A>0)的图象如图所示. 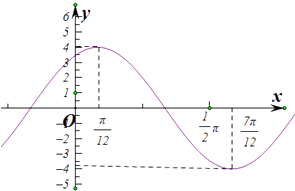
(1)求函数f(x)的解析式;
(2)写出函数f(x)的单调递增区间
(3)设不相等的实数,x1 , x2∈(0,π),且f(x1)=f(x2)=﹣2,求x1+x2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图所示的程序框图 
(1)当输入的x为2,﹣1时,分别计算输出的y值,并写出输出值y关于输入值x的函数关系式;
(2)当输出的结果为4时,求输入的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中,正确的有( ) ①两个变量间的相关系数r越小,说明两变量间的线性相关程度越低;
②命题“x∈R,使得x2+x+1<0”的否定是:“对x∈R,均有x2+x+1>0”;
③命题“p∧q为真”是命题“p∨q为真”的必要不充分条件;
④若函数f(x)=x3+3ax2+bx+a2在x=﹣1有极值0,则a=2,b=9或a=1,b=3.
A.0 个
B.1 个
C.2 个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分) 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过![]() ):
):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
|
|
|
|
该社团将该校区在![]() 年
年![]() 天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
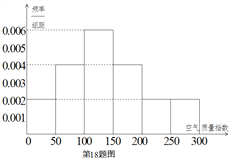
(Ⅰ)请估算![]() 年(以
年(以![]() 天计算)全年空气质量优良的天数(未满一天按一天计算);
天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)该校![]() 年
年![]() 月
月![]() 、
、![]() 日将作为高考考场,若这两天中某天出现
日将作为高考考场,若这两天中某天出现![]() 级重度污染,需要净化空气费用
级重度污染,需要净化空气费用![]() 元,出现
元,出现![]() 级严重污染,需要净化空气费用
级严重污染,需要净化空气费用![]() 元,记这两天净化空气总费用为
元,记这两天净化空气总费用为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com