【题目】已知如图所示的程序框图 
（1）当输入的x为2，﹣1时，分别计算输出的y值，并写出输出值y关于输入值x的函数关系式；
（2）当输出的结果为4时，求输入的x的值．
【答案】
（1）解：当输入的x为2时，y=log22=1，
当输入的x为﹣1时，y=（ 
）﹣1=2．
输出值y关于输入值x的函数关系式为：y=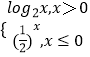 
（2）解：当x＞0时，y=log2x=4，解得：x=16；
当x≤0时，y=（ ）x=4，解得：x=﹣2．
综上，当输出的结果为4时，求输入的x的值为16或﹣2
【解析】（1）分析程序中各变量、各语句的作用，再根据图示的顺序，可知：该程序的作用是计算分段函数y=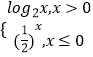 
的函数值，代入即可求值得解．（2）分段讨论，利用函数解析式，分别求出相应的x的值即可得解．
【考点精析】解答此题的关键在于理解程序框图的相关知识，掌握程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分：表示相应操作的程序框；带箭头的流程线；程序框外必要文字说明．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】设f（x）是定义在R上的增函数，且对于任意的x都有f（﹣x）+f（x）=0恒成立，如果实数a，b满足不等式组 
，那么a2+b2的取值范围是（ ）
A.[9，49]
B.（17，49]
C.[9，41]
D.（17，41]
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某早餐店每天制作甲、乙两种口味的糕点共n(nN*)份,每份糕点的成本1元,售价2元,如果当天卖不完,剩下的糕点作废品处理.该早餐店发现这两种糕点每天都有剩余,为此整理了过往100天这两种糕点的日销量(单位:份),得到如下的统计数据：
甲口味糕点日销量 | 48 | 49 | 50 | 51 |
天数 | 20 | 40 | 20 | 20 |
乙口味糕点日销量 | 48 | 49 | 50 | 51 |
天数 | 40 | 30 | 20 | 10 |
以这100天记录的各销量的频率作为各销量的概率,假设这两种糕点的日销量相互独立.
(1)记该店这两种糕点每日的总销量为X份,求X的分布列
(2)早餐店为了减少浪费,提升利润,决定调整每天制作糕点的份数
①若产生浪费的概率不超过0.6,求n的最大值;
②以销售这两种糕点的日总利润的期望值为决策依据,在每天所制糕点能全部卖完与n=98之中选其一,应选哪个？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)=(x-3)ex+ax,aR
(1)当a=1时,求曲线f(x)在点(2,f(2))处的切线方程；
(2)当a[0,e)时,设函数f(x)在(1,+)上的最小值为g(a),求函数g(a)的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
： 
的两个焦点与短轴的一个端点是直角三角形的三个顶点，直线
： 
与椭圆
有且只有一个公共点．
（Ⅰ）求椭圆
的方程及点
的坐标；
（Ⅱ）设
是坐标原点，直线
平行于
，与椭圆
交于不同的两点
、
，且与直线
交于点
，证明：存在常数
，使得
，并求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设向量 
=（sin 
x，cos x）， 
=（sin x， 
sin x），x∈R，函数f（x）= 
，求：
（1）f（x）的最小正周期；
（2）f（x）在区间[0，1]上的最大值和最小值，以及取得最大值和最小值时x的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
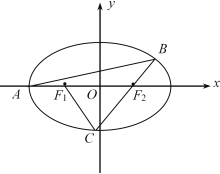
【题目】如图，已知椭圆
的左顶点
，且点
在椭圆上， 
、
分别是椭圆的左、右焦点。过点
作斜率为
的直线交椭圆
于另一点
，直线
交椭圆
于点
.
（1）求椭圆
的标准方程；
（2）若
为等腰三角形，求点
的坐标；
（3）若
，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=sinx﹣cosx+x+1，x∈[0，2π]
（1）求函数f（x）的单调递减区间；
（2）求函数f（x）的极小值和最大值，并写明取到极小值和最大值时分别对应x的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
