
【题目】已知定义在R上的函数f(x)=Asin(ωx+φ)(x>0,A>0)的图象如图所示. 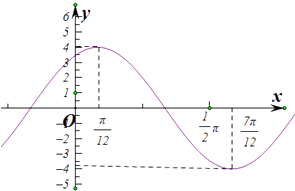
(1)求函数f(x)的解析式;
(2)写出函数f(x)的单调递增区间
(3)设不相等的实数,x1 , x2∈(0,π),且f(x1)=f(x2)=﹣2,求x1+x2的值.
【答案】
(1)解:由函数f(x)的图象可得A=4,
又∵函数的周期T=2( ![]() ﹣
﹣ ![]() )=π,
)=π,
∴ω═ ![]() =2,
=2,
∵函数图象经过点P( ![]() ,4),即:4sin(2×
,4),即:4sin(2× ![]() +φ)=4,
+φ)=4,
∴利用五点作图法可得:2× ![]() +φ=
+φ= ![]() ,求得:φ=
,求得:φ= ![]() ,
,
∴函数的表达式为: ![]()
(2)解:由2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,可得:kπ﹣
,k∈Z,可得:kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
可得函数f(x)的单调递增区间为: ![]()
(3)解:∵x∈(0,π),
∴2x+ ![]() ∈(
∈( ![]() ,
, ![]() ),
),
又∵f(x)=﹣2,可得:sin(2x+ ![]() )=﹣
)=﹣ ![]() ,
,
∴2x+ ![]() =
= ![]() 或
或 ![]() ,解得:x=
,解得:x= ![]() 或
或 ![]() ,
,
∴x1+x2= ![]()
【解析】(1)根据函数的最值得到A,再由函数的周期为2( ![]() ﹣
﹣ ![]() )=π,结合周期公式得到ω的值,再根据函数的最大值对应的x值,代入并解之得φ,从而得到函数的表达式.(2)由2kπ﹣
)=π,结合周期公式得到ω的值,再根据函数的最大值对应的x值,代入并解之得φ,从而得到函数的表达式.(2)由2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,可解得f(x)的单调递增区间.(3)由题意可得2x+
,k∈Z,可解得f(x)的单调递增区间.(3)由题意可得2x+ ![]() ∈(
∈( ![]() ,
, ![]() ),又f(x)=﹣2,可得:sin(2x+
),又f(x)=﹣2,可得:sin(2x+ ![]() )=﹣
)=﹣ ![]() ,进而解得符合条件的不相等的2个实数解,即可得解.
,进而解得符合条件的不相等的2个实数解,即可得解.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(1)求![]() 到平面
到平面![]() 的距离
的距离
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD及其三视图如下图所示,E是侧棱PC上的动点.
(Ⅰ)求四棱锥P﹣ABCD的体积;
(Ⅱ)不论点E在何位置,是否都有BD⊥AE?试证明你的结论;
(Ⅲ)若点E为PC的中点,求二面角D﹣AE﹣B的大小.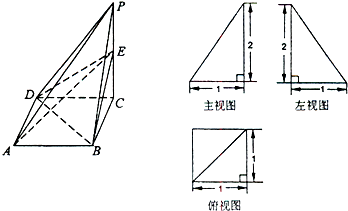
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某早餐店每天制作甲、乙两种口味的糕点共n(nN*)份,每份糕点的成本1元,售价2元,如果当天卖不完,剩下的糕点作废品处理.该早餐店发现这两种糕点每天都有剩余,为此整理了过往100天这两种糕点的日销量(单位:份),得到如下的统计数据:
甲口味糕点日销量 | 48 | 49 | 50 | 51 |
天数 | 20 | 40 | 20 | 20 |
乙口味糕点日销量 | 48 | 49 | 50 | 51 |
天数 | 40 | 30 | 20 | 10 |
以这100天记录的各销量的频率作为各销量的概率,假设这两种糕点的日销量相互独立.
(1)记该店这两种糕点每日的总销量为X份,求X的分布列
(2)早餐店为了减少浪费,提升利润,决定调整每天制作糕点的份数
①若产生浪费的概率不超过0.6,求n的最大值;
②以销售这两种糕点的日总利润的期望值为决策依据,在每天所制糕点能全部卖完与n=98之中选其一,应选哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆F1:(x+1)2+y2=16,定点F2(1,0),A是圆F1上的一动点,线段F2A的垂直平分线交半径F1A于P点.
(1)求P点的轨迹C的方程;
(2)四边形EFGH的四个顶点都在曲线C上,且对角线EG,FH过原点O,
若kEGkFH=-![]() ,求证:四边形EFGH的面积为定值,并求出此定值.
,求证:四边形EFGH的面积为定值,并求出此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线
的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线![]() :
: ![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
(Ⅰ)求椭圆![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(Ⅱ)设![]() 是坐标原点,直线
是坐标原点,直线![]() 平行于
平行于![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且与直线
,且与直线![]() 交于点
交于点![]() ,证明:存在常数
,证明:存在常数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家“十三五”计划,提出创新兴国,实现中国创新,某市教育局为了提高学生的创新能力,把行动落到实处,举办一次物理、化学综合创新技能大赛,某校对其甲、乙、丙、丁四位学生的物理成绩(x)和化学成绩(y)进行回归分析,求得回归直线方程为y=1.5x﹣35.由于某种原因,成绩表(如表所示)中缺失了乙的物理和化学成绩.
甲 | 乙 | 丙 | 丁 | |
物理成绩(x) | 75 | m | 80 | 85 |
化学成绩(y) | 80 | n | 85 | 95 |
综合素质 | 155 | 160 | 165 | 180 |
(1)请设法还原乙的物理成绩m和化学成绩n;
(2)在全市物理化学科技创新比赛中,由甲、乙、丙、丁四位学生组成学校代表队参赛.共举行3场比赛,每场比赛均由赛事主办方从学校代表中随机抽两人参赛,每场比赛所抽的选手中,只要有一名选手的综合素质分高于160分,就能为所在学校赢得一枚荣誉奖章.若记比赛中赢得荣誉奖章的枚数为ξ,试根据上表所提供数据,预测该校所获奖章数ξ的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxsin(x+ ![]() )﹣a,且x=﹣
)﹣a,且x=﹣ ![]() 是方程f(x)=0的一个解.
是方程f(x)=0的一个解.
(1)求实数a的值及函数f(x)的最小正周期;
(2)求函数f(x)的单调递减区间;
(3)若关于x的方程f(x)=b在区间(0, ![]() )上恰有三个不相等的实数根x1 , x2 , x3 , 直接写出实数b的取值范围及x1+x2+x3的取值范围(不需要给出解题过程)
)上恰有三个不相等的实数根x1 , x2 , x3 , 直接写出实数b的取值范围及x1+x2+x3的取值范围(不需要给出解题过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com