
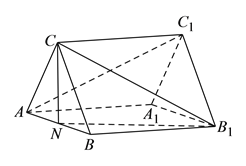
【题目】已知:正三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为棱
为棱![]() 的中点.
的中点.
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
(![]() )求四棱锥
)求四棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】试题分析:
(1)要证线面平行,就是要证线线平行,考虑过直线![]() 的平面
的平面![]() 与平面
与平面![]() 的交线
的交线![]() (其中
(其中![]() 是
是![]() 与
与![]() 的交点),而由中位线定理易得
的交点),而由中位线定理易得![]() ,从而得线面平行;
,从而得线面平行;
(2)由于![]() 是正三角形,因此有
是正三角形,因此有![]() ,从而只要再证
,从而只要再证![]() 与平面
与平面![]() 内另一条直线垂直即可,这可由正棱柱的侧棱与底面垂直得到,从而得线面垂直,于是有面面垂直;
内另一条直线垂直即可,这可由正棱柱的侧棱与底面垂直得到,从而得线面垂直,于是有面面垂直;
(3)要求四棱锥的体积,由正三棱柱的性质知![]() 中,边
中,边![]() 的高就是四棱锥的高,再求得四边形
的高就是四棱锥的高,再求得四边形![]() 的面积,即可得体积.
的面积,即可得体积.
试题解析:
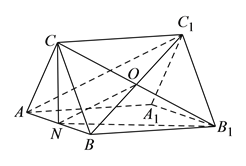
(![]() )证明:连接
)证明:连接![]() ,交
,交![]() 于
于![]() 点,连接
点,连接![]() ,
,
∵在![]() 中,
中,
![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 中点,
中点,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
(![]() )证明:∵在等边
)证明:∵在等边![]() 中,
中,
![]() 是棱
是棱![]() 中点,
中点,
∴![]() ,
,
又∵在正三棱柱中,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 点,
点,
![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(![]() )作
)作![]() 于
于![]() 点,
点,
∴![]() 是四棱锥
是四棱锥![]() 高,
高,
![]() ,
,
底面积![]() ,
,
![]() .
.


科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() 与圆
与圆![]() 相切,且交椭圆
相切,且交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 是椭圆的半焦距,
是椭圆的半焦距, ![]() .
.
(1)求![]() 的值;
的值;
(2)![]() 为坐标原点,若
为坐标原点,若![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(3)在(2)的条件下,设椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() ,
, ![]() ,动点
,动点![]() ,直线
,直线![]() ,
, ![]() 与直线
与直线![]() 分别交于
分别交于![]() ,
, ![]() 两点,求线段
两点,求线段![]() 的长度的最小值.
的长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两条不重合的直线![]() 和两个不重合的平面
和两个不重合的平面![]() ,若
,若![]() ,则下列四个命题:①若
,则下列四个命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() ; ③若
; ③若![]() ,则
,则![]() ;④若
;④若![]() ,则
,则![]() ,其中正确命题的个数是( )
,其中正确命题的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且和直线
且和直线![]() 相切,记动圆的圆心
相切,记动圆的圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设曲线![]() 上一点
上一点![]() 的横坐标为
的横坐标为![]() ,过
,过![]() 的直线交
的直线交![]() 于一点
于一点![]() ,交
,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于另一点
于另一点![]() ,若
,若![]() 是
是![]() 的切线,求
的切线,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校随机抽取100名学生调查寒假期间学生平均每天的学习时间,被调查的学生每天用于学习的时间介于1小时和11小时之间,按学生的学习时间分成5组:第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() ,第五组
,第五组![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
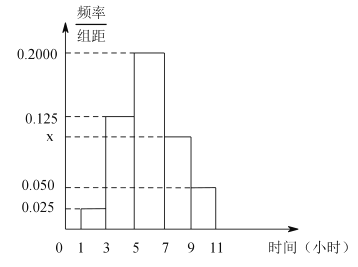
(1)求学习时间在![]() 的学生人数;
的学生人数;
(2)现要从第三组、第四组中用分层抽样的方法抽取6人,从这6人中随机抽取2人交流学习心得,求这2人中至少有1人学习时间在第四组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=x2+(a+2)x﹣3,x∈[a,b]的图象关于直线x=1对称.
(1)求a、b的值和函数的零点
(2)当函数f(x)的定义域是[0,3]时,求函数f(x)的值域..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据国家环保部最新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米。某城市环保部分随机抽取的一居民区过去20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
组别 | PM2.5平均浓度 | 频数 | 频率 |
第一组 | (0,25] | 3 | 0.15 |
第二组 | (25,50] | 12 | 0.6 |
第三组 | (50,75] | 3 | 0.15 |
第四组 | (75,100] | 2 | 0.1 |
(Ⅰ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(II)求样本平均数,并根据样本估计总计的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com