
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
已知命题p:“任意x∈R时,都有x2-x+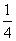 >0”;命题q:“存在x∈R,使sinx+cosx=
>0”;命题q:“存在x∈R,使sinx+cosx=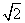 成立”.则下列判断正确的是( )
成立”.则下列判断正确的是( )
A.命题q为假命题 B.命题P为真命题
C.p∧q为真命题 D. p∨q是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
椭圆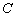 的中心为坐标原点
的中心为坐标原点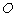 ,点
,点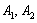 分别是椭圆的左、右顶点,
分别是椭圆的左、右顶点,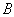 为椭圆的上顶点,一个焦点为
为椭圆的上顶点,一个焦点为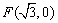 ,离心率为
,离心率为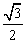 .点
.点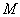 是椭圆
是椭圆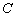 上在第一象限内的一个动点,直线
上在第一象限内的一个动点,直线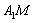 与
与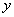 轴交于点
轴交于点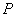 ,直线
,直线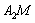 与
与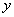 轴交于点
轴交于点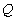 .
.
(I)求椭圆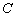 的标准方程;
的标准方程;
(II)若把直线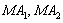 的斜率分别记作
的斜率分别记作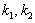 ,求证:
,求证: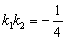 ;
;
(III) 是否存在点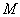 使
使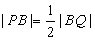 ,若存在,求出点
,若存在,求出点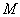 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
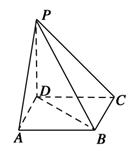
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(1) 证明PA⊥BD;
(2) 设PD=AD=1,求棱锥D-PBC的高.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com