
分析 根据题意,分析可得c=5,b=4,分2种情况讨论:即双曲线的焦点在x轴上和焦点在y轴上,求出a的值,将其代入双曲线的标准方程即可得答案.
解答 解:根据题意,要求双曲线的焦距是10,虚轴长是8,
则c=5,b=4,
分2种情况讨论:
①、双曲线的焦点在x轴上,
则有a2=c2-b2=9,
则双曲线的标准方程为:$\frac{x^2}{9}-\frac{y^2}{16}=1$;
②、双曲线的焦点在y轴上,
则有a2=c2-b2=9,
则双曲线的标准方程为$\frac{y^2}{9}-\frac{x^2}{16}=1$;
故答案为:$\frac{x^2}{9}-\frac{y^2}{16}=1$或$\frac{y^2}{9}-\frac{x^2}{16}=1$.
点评 本题考查双曲线的几何性质,注意区分双曲线焦点的位置.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
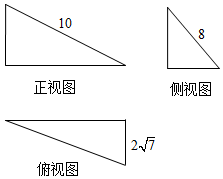
| A. | 32 | B. | $32\sqrt{7}$ | C. | $16\sqrt{7}$ | D. | $64\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
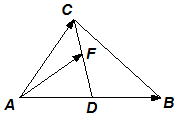 如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}$+$\frac{4}{y+1}$的最小值为3+2$\sqrt{2}$.
如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}$+$\frac{4}{y+1}$的最小值为3+2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
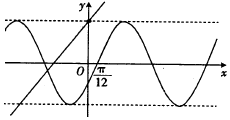 已知函数y=ksin(kx+φ)(|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则φ=-$\frac{π}{6}$.
已知函数y=ksin(kx+φ)(|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则φ=-$\frac{π}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{21}{4}$ | C. | $\frac{17}{4}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
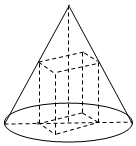 底面半径为3,高为$6\sqrt{2}$的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).
底面半径为3,高为$6\sqrt{2}$的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com