
多面体ABCDEF的直观图及三视图分别如图所示,已知点M在AC上,点N在DE上,且AM:MC=DN:NE=a
(1)求证:MN//平面BCEF;
(2)当a=1时,求二面角D―MN―F的余弦值的绝对值。


解:(1)由三视图可知,该多面体是底面为直角三角形的直三棱柱ABF―DCE。
且AB=BC=AF=2,CE=BF=![]() ,∠BAF=90°
,∠BAF=90°
在CD上取一点G,DG:GC=DN:NE,连MG、NG。则
∵AM:MC=DN:NE=a,
∴NG//CE,MG//BC。
∴平面MNG//平面BCEF。
∴MN//平面CDEF。
(2)∵a=1
∴M、N分别是AC、CE的中点。
以AB、AF、AD分别为x轴、y轴、z轴,建立空间直角坐标系,则有关各点的坐标分别是D(0,0,2),F(0,2,0),M(1,1),N(0,1,2)
∴![]()
设平面DMN的法向量![]()
∴![]()
∴![]()
∴![]()
设平面MNF的法向量为![]()
∴
∴![]()
设二面角D―MNF的平面角为![]() ,
,
则
![]()
∴二面角D―MN―F的余弦值的绝对值为![]() 。
。


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
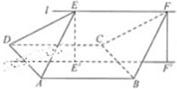 如图,ABCD的边长为2的正方形,直线l与平面ABCD平行,E和F是l上的两个不同点,且EA=ED,FB=FC,E′和F′是平面ABCD内的两点,E′E和F′F都与平面ABCD垂直,
如图,ABCD的边长为2的正方形,直线l与平面ABCD平行,E和F是l上的两个不同点,且EA=ED,FB=FC,E′和F′是平面ABCD内的两点,E′E和F′F都与平面ABCD垂直,查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,ABCD是边长为3正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图正方形ABCD和四边形ADEF所在的平面垂直,FA⊥AD,DE∥FA,且AD=DE=
如图正方形ABCD和四边形ADEF所在的平面垂直,FA⊥AD,DE∥FA,且AD=DE=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.
如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com