
分析 (I)利用切线的性质列方程解出圆心坐标即可得出圆的方程;
(II)设直线l斜率为k,联立方程组,利用根与系数的关系计算x1x2,y1y2,根据数量积公式列方程解出k得出直线l的方程.
解答 解:(I)设圆C的圆心为C(a,0),
则C到直线3x-4y+4=0的距离等于圆的半径,
∴$\frac{|3a+4|}{\sqrt{9+16}}$=2,解得a=2或a=-$\frac{14}{3}$(舍).
∴圆C的方程为(x-2)2+y2=4.
(II)若直线l无斜率,则直线l方程为x=0,与圆C相切,不符合题意;
若直线l有斜率,设直线l的方程为y=kx-3,
联立方程组$\left\{\begin{array}{l}{y=kx-3}\\{(x-2)^{2}+{y}^{2}=4}\end{array}\right.$,得(1+k2)x2-(4+6k)x+9=0,
∵直线l与圆有两个交点,
∴△=(4+6k)2-36(1+k2)>0,解得k>$\frac{5}{12}$.
由根与系数的关系可得:x1+x2=$\frac{4+6k}{1+{k}^{2}}$,x1x2=$\frac{9}{1+{k}^{2}}$,
∴y1y2=(kx1-3)(kx2-3)=k2x1x2-3k(x1+x2)+9=$\frac{9{k}^{2}}{1+{k}^{2}}$-$\frac{12k+18{k}^{2}}{1+{k}^{2}}$+9=$\frac{9-12k}{1+{k}^{2}}$,
∵$\overrightarrow{OA}•\overrightarrow{OB}$=3,
∴x1x2+y1y2=3,即$\frac{9}{1+{k}^{2}}$+$\frac{9-12k}{1+{k}^{2}}$=3,解得k=1或k=-5(舍).
∴直线l的方程为y=x-3.
点评 本题考查了圆的标准方程,直线与圆的位置关系,距离公式的应用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{16}$ | B. | 7 | C. | 16 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
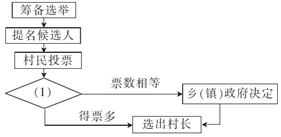 选举时常用的选举方式是差额选举(候选人多于当选人数),某村选举村长,具体方法是:筹备选举,由乡(镇)政府提名候选人,村民投票(同意,不同意,弃权),验票统计,得票多者选为村长;若票数相等,则由乡(镇)政府决定谁当选.下面的流程图表示该选举过程,则图(1)处应填的是验票统计.
选举时常用的选举方式是差额选举(候选人多于当选人数),某村选举村长,具体方法是:筹备选举,由乡(镇)政府提名候选人,村民投票(同意,不同意,弃权),验票统计,得票多者选为村长;若票数相等,则由乡(镇)政府决定谁当选.下面的流程图表示该选举过程,则图(1)处应填的是验票统计.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 平均车速超过100km/h人数 | 平均车速不超过100km/h人数 | 合计 | |
| 男性驾驶员人数 | |||
| 女性驾驶员人数 | |||
| 合计 | |||
| P(K2≥k0) | 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com