Question

16．已知函数f（x0=$\left\{\begin{array}{l}{{2}^{x}-1（x≤0）}\\{|x-1|-1（x＞0）}\end{array}\right.$．
（1）画出y=f（x）的图象，并指出函数的单调递增区间和递减区间；  
 （2）解不等式f（x-1）≤-$\frac{1}{2}$．

Answer 1

分析 （1）画图，由图象可得单调区间，
（2）分段求出不等式的解集即可．

解答 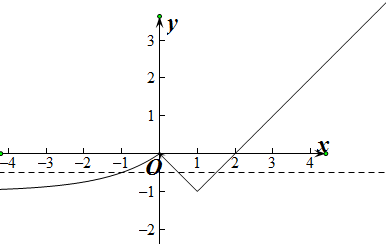解：（1）图象如图所示：由图象可知函数的单调递增区间为
（-∞，0），（1，+∞），
丹迪减区间是（0，1）
（2）由已知可得$\left\{\begin{array}{l}{{2}^{x}-1≤-\frac{1}{2}}\\{x≤0}\end{array}\right.$
或$\left\{\begin{array}{l}{|x-1|-1≤-\frac{1}{2}}\\{x＞0}\end{array}\right.$，
解得x≤-1或$\frac{1}{2}$≤x≤$\frac{3}{2}$，
故不等式的解集为（-∞，-1]∪
[$\frac{1}{2}$，$\frac{3}{2}$]．

点评 本题考查了分段函数的图象的画法和不等式的解集的求法，属于基础题．